以下の文章の【 】に適当な数式を入れよ。
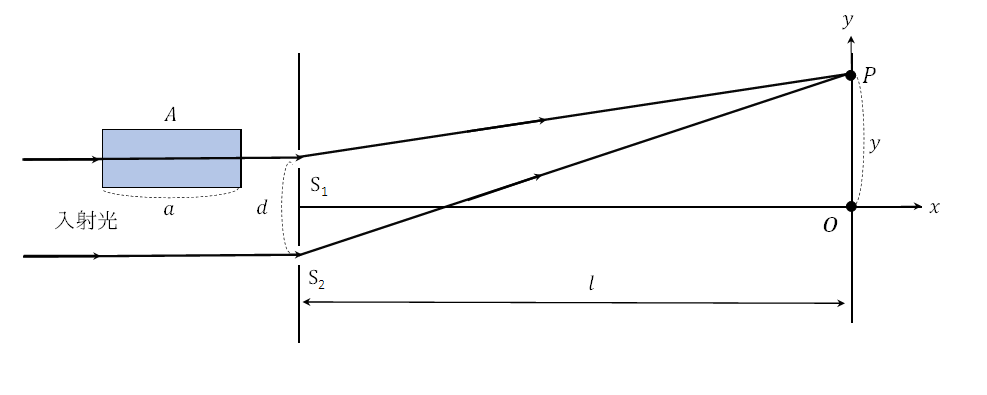
図のように、真空中に間隔 \(d\) の2つのスリット \(S_{1}\),\(S_{2}\) を置き、さらにスリットから \(l\) 離れた位置に、\(S_{1}\),\(S_{2}\)に平行スクリーンを置く。\(S_{1}\)\(S_{2}\)の垂直二等分線を \(x\) 軸にとり、\(x\) 軸とスクリーンが交わる点を原点 \(O\) としてして、図のように \(y\) 軸を取る。スリット \(S_{1}\) の手前(スクリーンの反対側)には、 \(x\) 軸に垂直な断面をもち、屈折率を自由に変えられる長さ \(a\) の透明な媒質 \(A\) が置かれている。ただし、\(A\) の表面での光の反射は無視できるものとする。
(1)
真空中の波長が \(λ\) の単色光平面波を \(x\) 軸を平行に \(S_{1}\),\(S_{2}\) に入射する。真空中の光の速さを \(c\) とすると、入射光の振動数は【 1 】である。媒質Aの屈折率が \(n\) のとき、\(A\) の中を進光の速さは \(c\) の \(1/n\) 倍となる。振動数は媒質中でも変わらないので、\(A\) の中を進む光の波長は \(λ\) の【 2 】倍となる。\(A\) の中を光が \(a\) 進むのにかかる時間は【 3 】であり、同じ時間に真空中の光は【 4 】進む。\(S_{1}\),\(S_{2}\) で回折した光は互いに干渉し、スクリーン上に明暗の縞模様を描く。\(A\) の屈折率が1のとき、点 \(O\) および点 \(O\) の両側に等しい間隔で明暗が観測された。点 \(O\) の明線を0次、点 \(O\) の両側の明線を、点 \(O\) に近い方から順に1次、2次、3次、・・・の明線と呼ぶことにする。点 \(O\) から \(m\)次(\(m\) =0,1,2,・・・)の明線までの距離を \(y_{m}\) とすると、両スリットから \(m\) 次の明線までの経路差は、\(d\) および \(y_{m}\) が \(l\) に比べて十分に小さいものとして、\(\begin{eqnarray}\frac{dy_{m}}{l} \\[ 5pt ] \end{eqnarray}\)で与えられる。したがって、\(y_{m}\) =【 5 】となり、隣りあう明線と明線の間隔は、【 6 】と求められる。
(2)
\(A\) の屈折率を時刻 \(t\) =0 で 1 とし、その後、単位時間あたり \(r\) の割合で増加させたところ、干渉縞は \(y\) 軸縞は \(y\) 軸正の向きに移動した。屈折率が \(n\) になったときに、最初点 \(O\) にあった明線は点 \(P\) まで移動した。このとき、経路差\(\overline{S_{2}P}-\overline{S_{1}P}\)と、\(A\) によって生じる光路差 \((n-1)a\) が等しくなる条件より、点 \(P\)の位置は、\(y\)=【 7 】と求められる。明線と明線の間隔は変化しないので、\(m\) 次の明線が点 \(O\) をよぎる時刻を\(t_{m}\)とすると、\(r\)\(t_{m}\)\(a\)=【 8 】の関係が成り立つ。したがって、点 \(O\)をよぎる明線の数は、単位時間あたり【 9 】個となる。
(北海道大)
【問題PDF】
【解説】


【解説PDF】




コメント