水面上で \(l\)0〔cm〕離れた2点 S1,S2 が振動し、ともに波長 λ〔cm〕,振幅 A〔cm〕,速さ\(v\)〔cm/s〕の球面波(円形波)を送り出している。図は波源を逆位相で振動させたときのある時刻の波の重なりあいを、山を実線、谷を破線として示してある。ただし、S1,S2 から出る波の振幅は波源からの距離によって変化しないものとする。
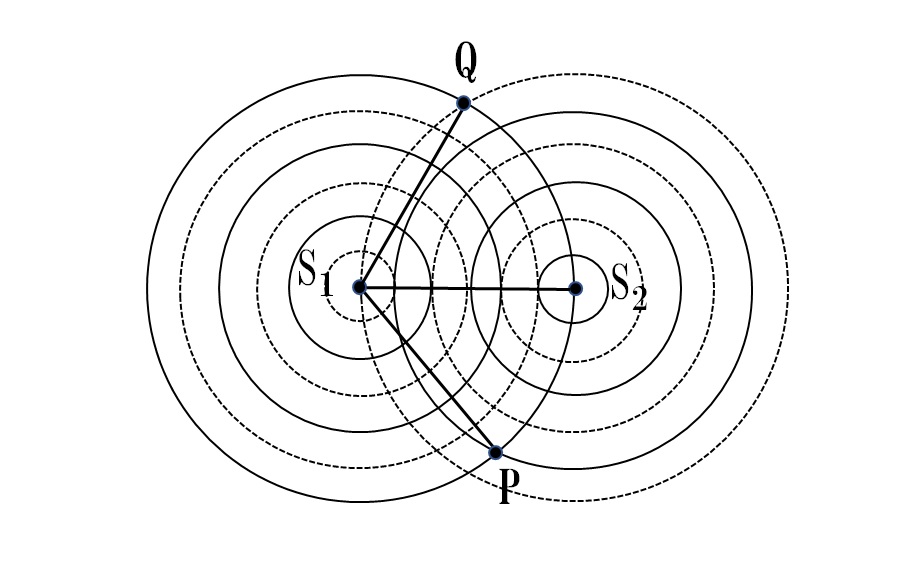
(a)図のP,Qの各点で2つの波は強め合うか、打ち消し合うか述べよ。
(b)(a)の根拠となる(イ)強め合う条件(ロ)打ち消し合う条件を波源S1,S2 からP点までの距離をそれぞれ \(l\)1,\(l\) 2 とし、同様に、波源S1,S2からQ点までの距離をそれぞれ \(l\)3,\(l\) 4として示せ。
(c)S1,S2の間の距離 \(l\) 0を9.00cm,波長 λ を3.00cm,振幅 A を0.5cm,球面波の速さ \(v\)を2.10×10 cm/s としたとき、図の時刻から半周期後の点P,点Qの水平面からの変位を求めよ。
(d)線分 S1S2 上にできる定常波の腹の位置すべてを S1 からの距離で示せ。
(e)振動数を 8.4Hz にし、同位相で2点 S1,S2を振動させたときには、線分 S1S2 上の定常波の腹は何点できるか求めよ。ただし、球面波の速さは変わらないとする。
【問題PDF】
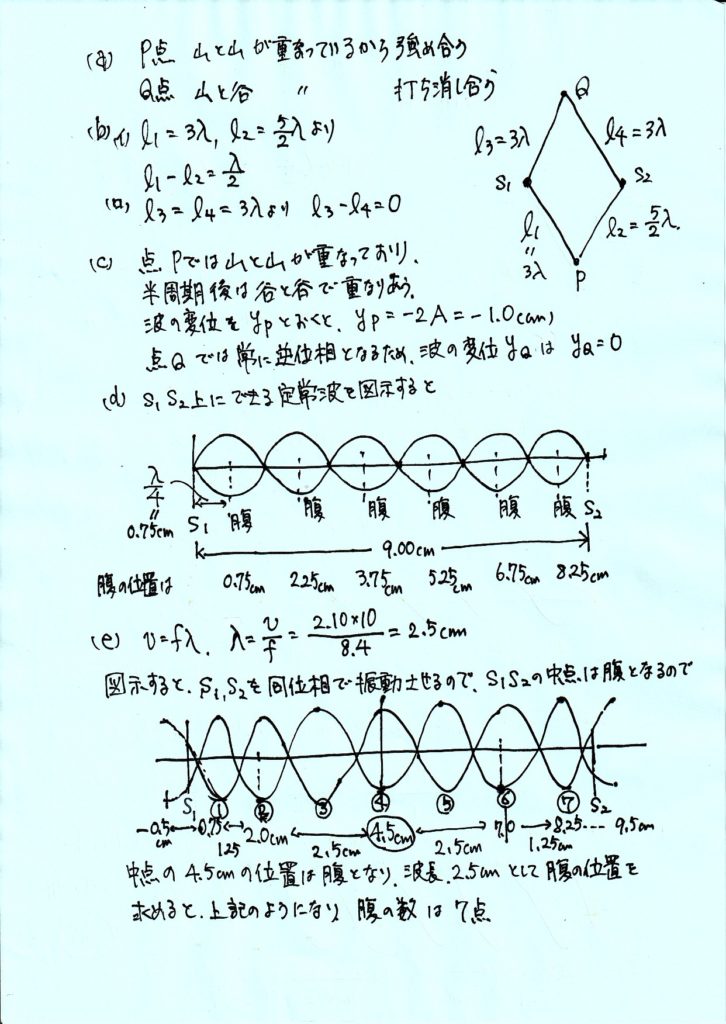
【解説PDF】




コメント