空気中に図のような正三角形状のプリズムが置かれている。
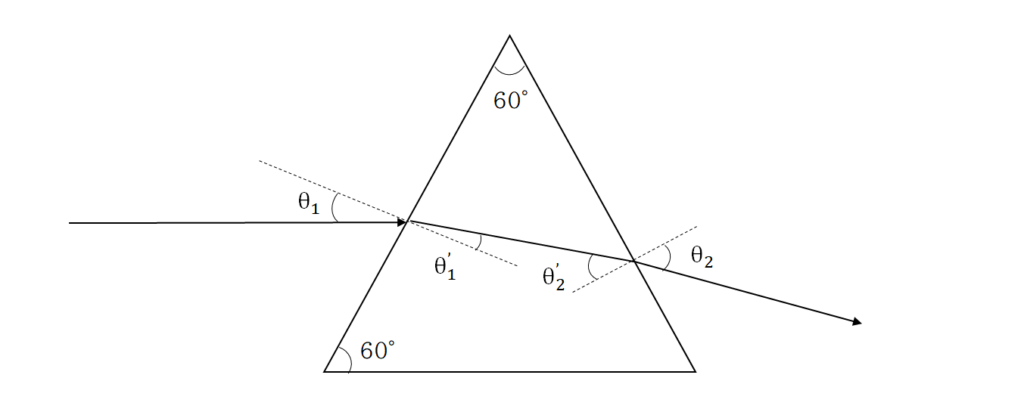
このプリズムに対し、三角形の底面に平行な単色光が入射する。
入射光に対する空気の屈折率を 1 、プリズムの屈折率を \(n\) とする。
入射面に垂直な線と入射光のなす角度は \(\theta _{1}\) ×【 ア 】であるから、屈折後のなす角度 \(\theta _{1}’\) に対し、\(\sin \theta _{1}’\) =【 イ 】が成り立つ。
一方、光がプリズムから出る際に、プリズムの内側での光と屈折面に垂直な線とのなす角を \(\theta _{2}\) とする。
このとき、\(\theta _{2}\) = 【 ウ 】― \(\theta _{1}\) であるから、
三角関数の加法定理を用いると、
\(\sin \theta _{1}’\) = \(\sin\)【 ウ 】\(\cos \theta _{1}’\) - \(\cos\) 【 ウ 】\(\sin \theta _{1}’\)
となる。
以上より、プリズムから出て行く光の角度 \(\theta _{2}\) について、\(\sin \theta _{2}\) =【 エ 】
の関係が成り立つ。
もし、プリズムの屈折率が 【 オ 】より大きければ、プリズムの右側面では、光は【 カ 】し、プリズムの右側面からは出てこなくなる。
問1 本文中の【 ア 】~【 カ 】に適当な値、式、もしくは語句を入れよ。
問2 白色光がプリズムに入射すると、プリズムから出る光はどうなるか。理由を付けて述べよ。
(新潟大)
【問題PDF】
【解説】
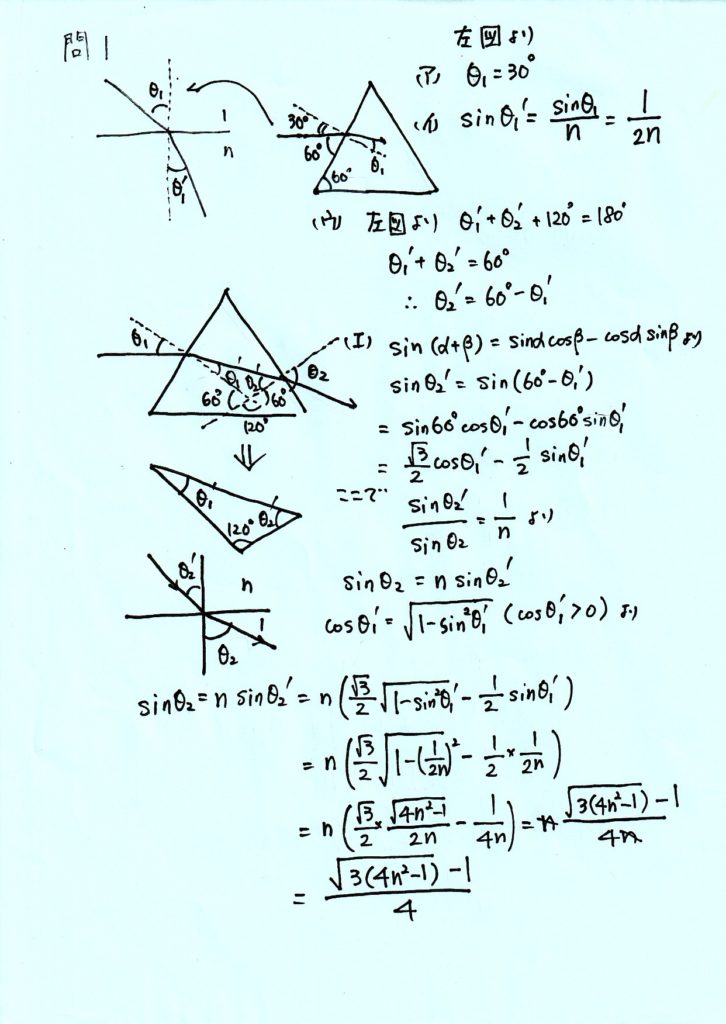
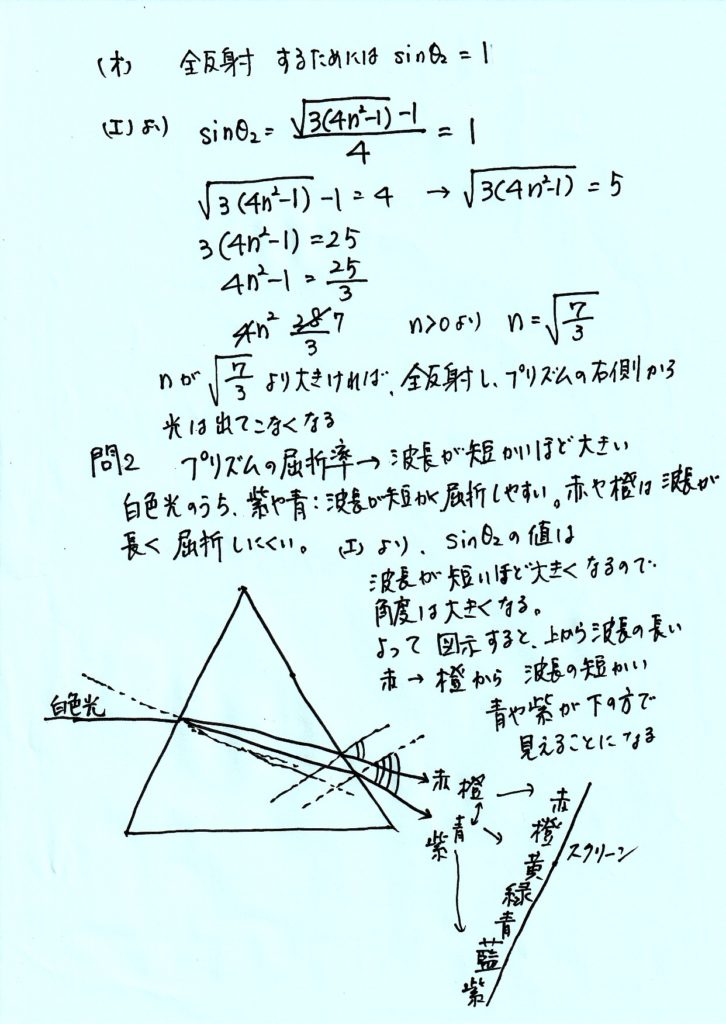
【解説PDF】



コメント