図1において、原点にある音源Pの振動が \( y= A \) \( sin\) \(at\) ( \(y\) は変位、\(t\)は時間)と表され、Pから出て+\(x\) 方向に伝わる音波が \( y = A\) \(sin\) \(( at – bt )\) と表されるとする。
時間 \(\Delta t \) の間に波が \(\Delta x \) だけ進むとすると、\(a , b , \Delta t , \Delta x \) の間には、【 1 】の関係が成り立つから、\(a\) と \(b\) の関係はグラフ【 2 】で表される。
いま、振動がPと全く同じく \(y=A\) \(sin\) \(at\) で表されるような音源Qを、\(x\) 軸上に置く。PとQの振動の開始時刻が等しいとき、\(x\) =\(L\) にある音波検出器Dで音波が検出されないようなPQ間の距離の中で最小のものは、\(d\) =【 3 】である。ただし、\(L>>d\) とする(図1)。 この位置で、Qの振動の開始の時刻をPより遅らせると、再びDで音波が検出されるが、遅れが【 4 】のときにDでは振幅 2\(A\) の音波が検出される。
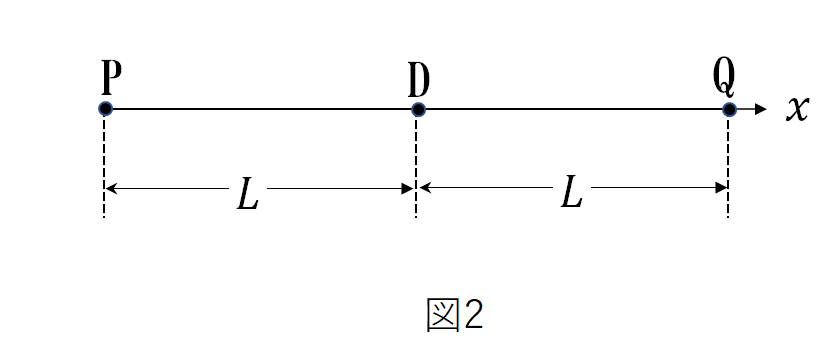
次に図2のようにQを \(x=2L\) に置き。PとQを同位相で振動させると、+\(x\) 方向に進むPの波と、-\(x\) 方向に進むQの波が出会って、Dにおいて合成波 \(Y\) =【 5 】が生じる。Dにおいて振幅が常に2\(A\) であったとすると、\(x\) 軸上で振幅が常に0になる点のうち、最もDに近い2点の座標は \(x = L \pm\)【 6 】である。
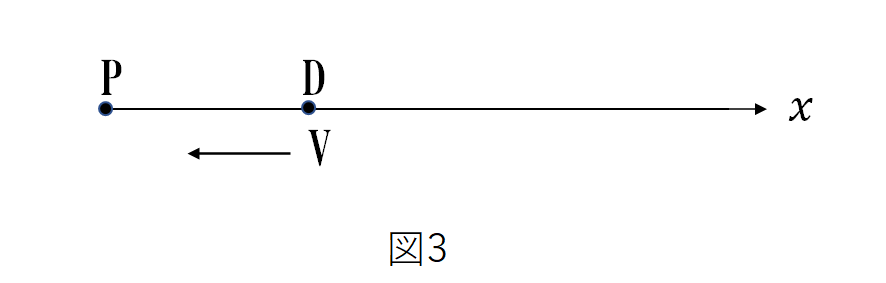
次にQを取り除き、図3のようにDをPに向けて一定速度 \(V\) で近づけるとき、Dで検出される音波の振動数はDが静止のときよりも大きくなる。その理由は、時間\(t\) の間にDが受ける波の数は、Dが静止していれば【 7 】であるのに、DがPに速さ \(V\) で近づくときには、【 8 】になるからである。
【問題PDF】
【解説】


【解説PDF】




コメント