観測者が、音源の横を通過するときに経験する音の周波数変化を、観測者に音の波が到達する時期から考察してみよう。音源Sと観測者は十分に離れており、それぞれが移動する速さは音速 \(V\)〔m/s〕に比べて十分に小さいとする。次の空欄に入る式を答えよ。
《 I 》
図1のように、観測者が音源から距離L,角度θの方向にある O 点から、音源に近づく方向に速さ\(u\)で移動しているとする。 ただし、θ が π/2 よりも小さい範囲を考える。観測者が O 点を通過したときに音波の振幅の山を観測し、次の音波の振幅の山を観測した地点が O’ であった。
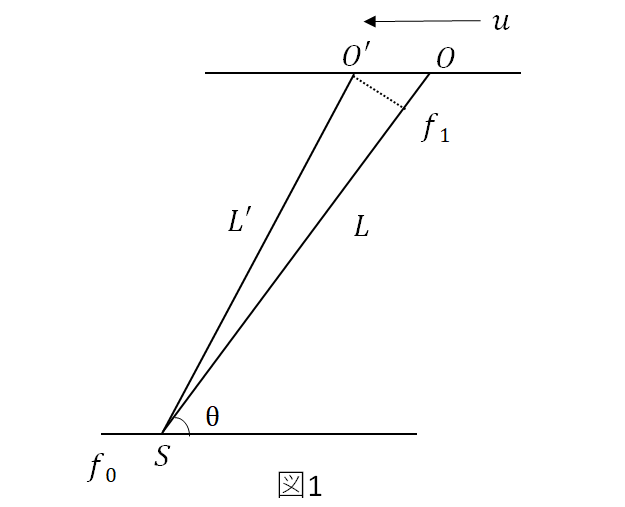
音源の周波数を f0,観測者の感じる音の周波数を f1 とすると、この間に経過した時間は【 1 】であるので、OO’=【 2 】と表すことができる。次に、音源から出た音波の伝わる様子を考える。時刻 0 に S から出た音波の山が 間の距離 L を進んで O に到達する時刻は t =【 3 】である。次の音波の山が の距離 L’ を進んで O‘ に到達する時刻は t’=【 4 】である。 今、L ,L’ が OO’ に比べて十分大きいとすると、L-L’ = OO’ cos θ と表すことができるので、t’ - t =【 5 】である。一方、この差は観測者が観測した【 1 】に等しいことを用いると f1=【 6 】を得ることができる。
《 II 》
次に、図2に示すように、音源 S も観測者も同じ方向に速さ \(v\) で運動している場合を考える。
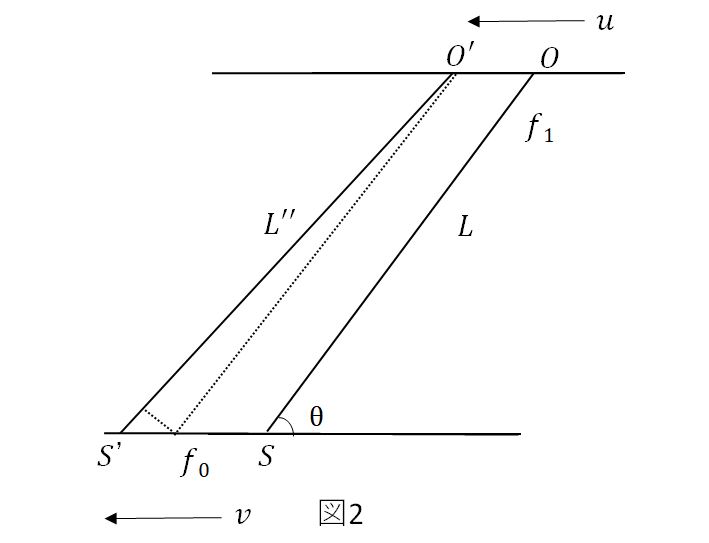
同様に、速さ \(u\) で移動している観測者が、音源から距離 L,角度 θ の方向にある O 点を通過したときに音波の振幅の山を観測し、次の音波の振幅の山を O’ で観測した。このとき観測者が感じる周波数を f2 とする。O 点については、《 I 》と同様に扱うことができる。一方、観測者が O’で観測した音波の振幅の山は、音源が S‘ の位置に移動したときに発せられ、S’O’ 間の距離 L’‘を進んで時刻 t’‘に到達したものである。すると、SS’=【 7 】である。同様に、SO と S’O’ との差は(SS’-OO’)×cosθと表せることを用いて、t’‘ -t =【 8 】を得る。これば観測者が観測した波の山と山との時間間隔【 9 】に等しいことを用いて、f2=【 10 】が得られる
【問題PDF】
【解説】


【解説PDF】


コメント