ある媒質中を進む波の様子を記録したところ、\(t=0 \)での波の様子は図1のように表された。
この波の式を定数 \(a, b\) を用いて
\( y=sin(at +bx) \) (A)
と表すこととする。 ただし、\( a \)>0とする。以下の問いに答えなさい。
(1)(A)の式の波の波長 \( λ \) ,周期 \(T\) ,および波の伝わる速さ\(v\) を \(a\) と\(b\) で表せ。
(2)(A)の式で\(b\)>0,\(b\) <0のそれぞれの場合において、波の進む方向を答えよ。
(3)図1の波がx軸正の向きに進む場合、\(x\) =0の点における波の変位を時間 \(t\) のグラフとしてその概形を描きなさい。
(4)次に、同じ媒質中に壁を設置したところ、入射波と反射波が重なりあって定常波がみられた。図2は、ある時刻での壁に対する入射波の様子を表している。このときの定常波の概形を描きなさい。ただし、壁での波の反射は固定端反射であるとする。
(5)(A)式を入射波として、反射波の式を求めよ。ただし、固定端の位置を \(x\) =0とする。
(6)(5)の結果から、定常波の式を求め、その最大の振幅を求めよ。ただし、
\( sin(A±B)=sinAcosB±cosAsinB \) を用いてよい。
(7)さらに、同じ媒質中で \(x\) =0,\(x=L\) の2カ所に壁を設置した。このとき定常波が存在するためのLの満たす条件を求めよ。
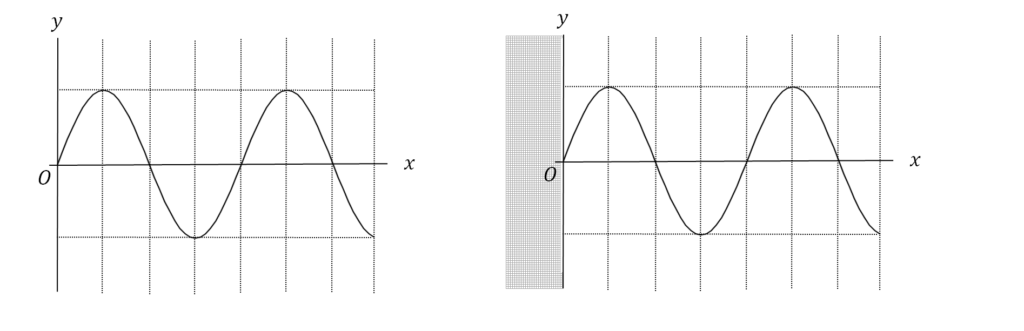
(図1) (図2)
(お茶の水女子大)
【問題PDF】
【解説】
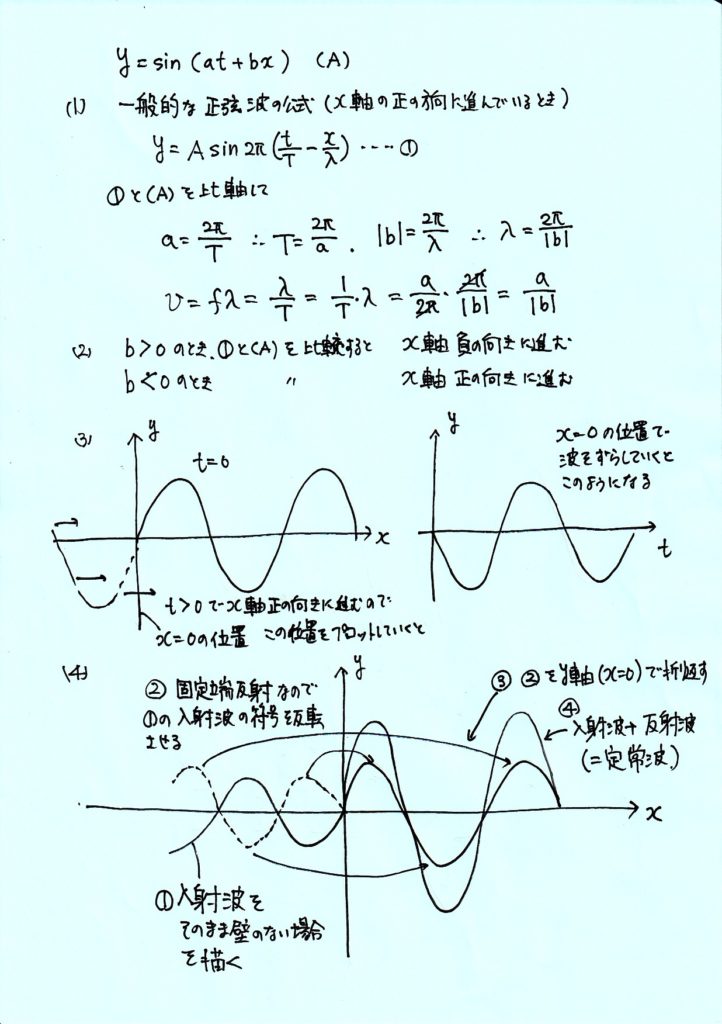

【解説PDF】


コメント