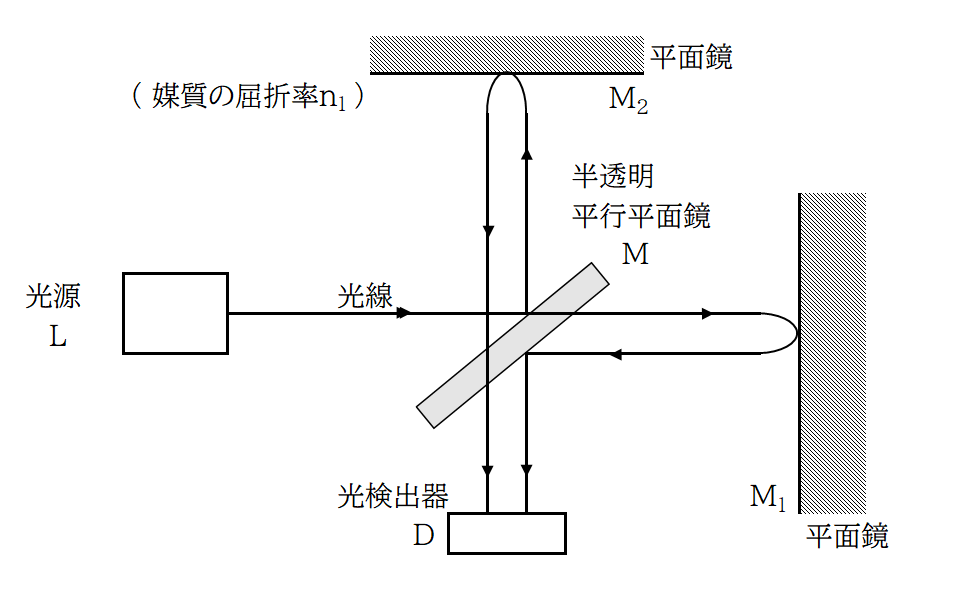
図において、Lは波長が真空中で λ0〔m〕の光源、Mは光源の一部を通し一部を反射する半透明平行平面鏡、M1 および M2 は、それぞれ、Mを通過した光源およびMで反射された光線に垂直に置かれた平面鏡である。D は光検出器であり、D には2つの光源すなわちMを通り M1で反射されさらに M で反射された光線と、M で反射されたあと M2 で再び反射されてからMを通過してきた光線が入る。D に入るこの2つの光線は干渉により強めあったり弱めあったりする。今、装置全体が屈折率 n1 の媒質の中に置かれており、2つの光線の間には光路差がなく強めあっているものとし、半透明平行平面鏡 M の厚さは無視できるものとする。
(1)屈折率 n1 の媒質においては、光の速さは真空中の光の速さの【 1 】倍であり、その振動数は真空中の振動数の【 2 】倍であるから、波長が真空中で λ0〔m〕の光源の波長は【 3 】× λ0〔m〕である。
(2)図の状態で M と M1 の間に屈折率 n2(>n1)で厚さ t〔m〕の平行平面膜を光線に垂直に置いたとき、2つの光線の間の光路差は【 4 】×t〔m〕となる。
(3)また、図の状態から M1 を d〔m〕だけゆっくりと M の方向に平行移動したとき、2つの光線の間の光路差は【 5 】〔m〕となる。このとき、2つの光線は検出器で m 回目の強めあう状態になった。m の値は d,n1 と λ0 で表すと【 6 】である。
(4)(3)において、媒質を屈折率 1.0 の空気とし、真空中の波長が λ1 と λ2 の2種類の光源(ただし、λ2 は未知)について、M1 の移動距離を同じにして強めあう回数 m1 ,m2 を測定した。λ1 が6.3×10-7〔m〕 のとき m1 は3.2×103回であり、λ2 の場合、m2 は4.0×103回であった。この結果から、波長が未知である光源の真空中の波長 λ2 は【 7 】×10-7〔m〕である。
(近畿大)
【問題PDF】
【解説】

【解説PDF】



コメント