図1のように、 \(x\) 軸の正の向きに伝わる正弦波の縦波がある。波が伝わるとき、媒質はそのつりあい位置から変位する。縦波は、その変位が波の進行方向と同じなので、横波に比べて波の状態がわかりにくい。そこで図1では、媒質が \(x\) 軸の正の向きに変位したときは、\(y\) 軸の正の向きに、\(x\) 軸の負の向きに変位したときは \(y\) 軸の負の向きに変位をとることで、縦波を横波のように表した。
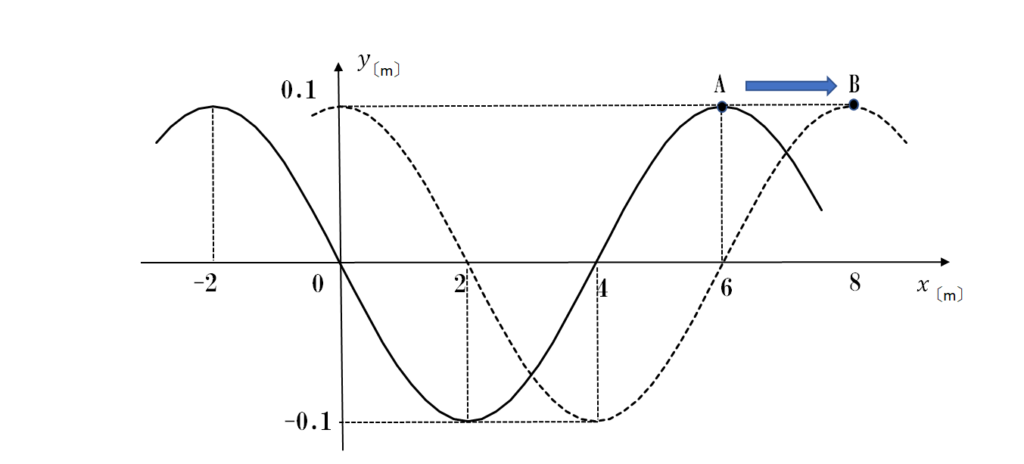
時刻 \(t\)〔s〕における媒質の変位を実線で示し、その0.02秒後の媒質の変位を破線で示してある。この波の山は0.02秒の間に点Aから点Bまで進んだ。
次の値を求めよ。
(ア)縦波の振幅:〔m〕
(イ)波長:〔m〕
(ウ)波の速さ:〔m/s〕
(エ)周期:〔s〕
(オ)振動数:〔Hz〕
図1を見ながら、媒質の疎密について考えてみる。
\(x\) 軸上の 0 \(\leq\) \(x\) \(\leq\) 6の範囲で、時刻 \(t\)〔s〕において
(カ)媒質が最も密な位置:\(x\) 〔m〕
(キ)最も疎な位置: \(x\)〔m〕
(ク)媒質の速さが右向きに最大となる位置:\(x\) 〔m〕
(ケ)媒質の速さが0の位置: \(x\)〔m〕と(コ)\(x\) 〔m〕
【問題PDF】
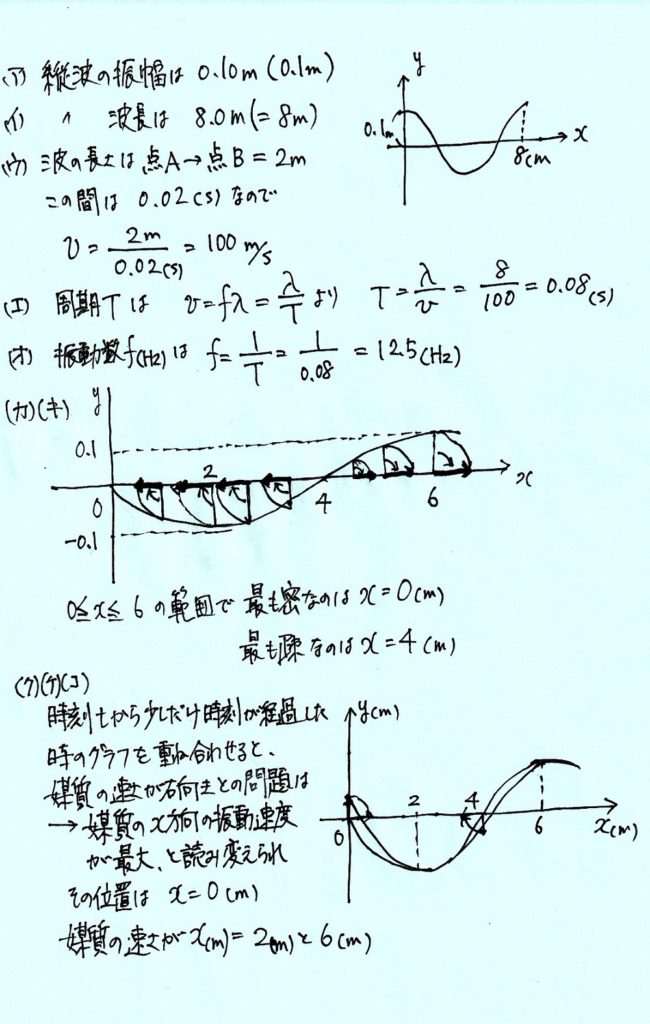
【解説PDF】



コメント