図のように、単原子分子の理想気体が入っているシリンダーAと円筒容器Bが、細い管でつながっている。
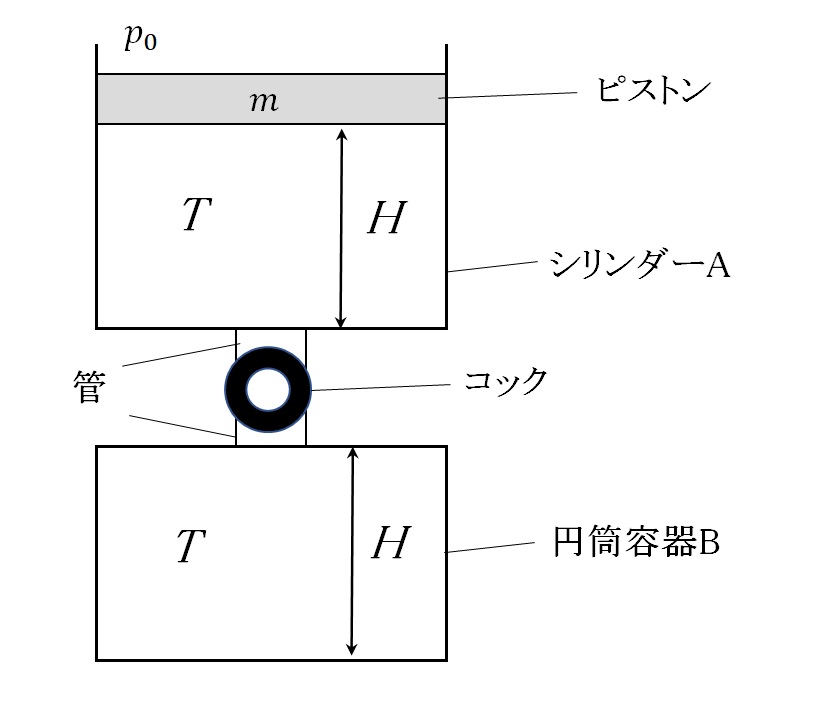
この管に取り付けてあるコックを開く前のシリンダーAと円筒容器Bの気体、ともに \(T\)〔K〕で、円筒容器B内の気体の圧力はシリンダーA内の圧力の \(\frac{14}{15}\) 倍である。鉛直方向に置かれたシリンダーAにはなめらかに動く断面積 \(S\)〔m2〕、質量 \(m\)〔kg〕のピストンが備わっている。コックを開く前のピストン下面の位置はシリンダ底面から \(H\)〔m〕の高さにある。コックをゆっくり開くと、ピストンの高さは \(xH\)〔m〕(0<\(x\) <1)に変化するが、断面積 \(S\)〔m2〕の円筒容器Bの高さは \(H\) のまま変化がない。 ただし、大気圧を \(p_{0}\) 〔Pa〕とする
この時、以下の空欄【 】に適した数式あるいは数値を答えよ。数式中の変数には、\(T\) , \(p_{0}\) ,\(S\) ,\(H\) ,\(m\) ,\(x\) を使用すること。必要があれば気体定数 \(R\)〔J/(mol・K)〕,重力加速度の大きさ \(g\)〔m/s2〕を使用してもよい。ただし、ピストン,シリンダーA,円筒容器B,管,コックそれぞれと外部との間の熱の移動はなく、管とコックそれぞれの容積は無視できるほど小さいとする。
コックを開く前のシリンダーA内の気体の圧力は 【 ア 】〔Pa〕であり、その量は 【 イ 】〔mol〕 である。また、このときの円筒容器B内の気体の量は【 ウ 】〔mol〕である。したがって、コックを開く前のシリンダーA内の気体の内部エネルギーは【 エ 】〔J〕で、円筒容器B内の気体の内部エネルギーは【 オ 】〔J〕である。
コックを開いてからシリンダーAと円筒容器B内の気体が熱平衡の状態になるまでに、気体に加えられた仕事は【 カ 】〔J〕であるので、熱力学の第1法則を適用すると、熱平衡後の気体の温度は【 キ 】〔K〕となる。また、同時に理想気体の状態方程式を満足することから、 \(x\) = 【 ク 】が得られる
(北九州市立大学)
【問題PDF】
【解説】


【解説PDF】

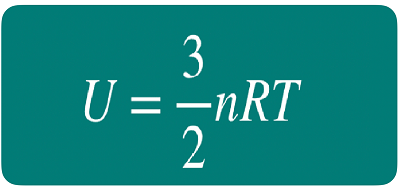


コメント