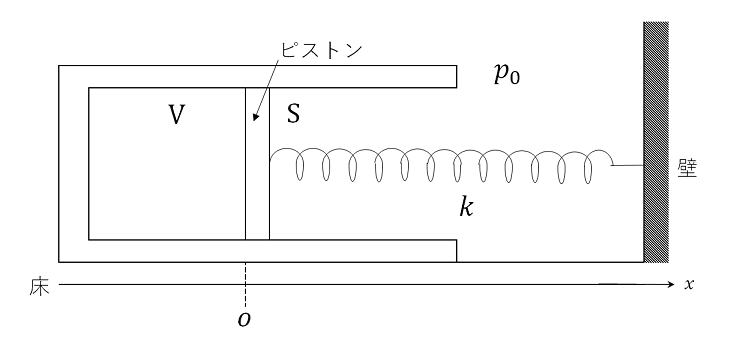
図のように、大気圧が \(p_{0}\)で一定の大気圧中で、ばね定数 \(k\) の軽いばねの一端を取り付けたピストンを用いて、断面積 \(S\) のシリンダーの内に単原子分子理想気体を封入し、シリンダーを床に固定する。ピストンは、シリンダーの内壁に沿って、水平方向になめらかに動くことができる。はじめ、シリンダー内の気体の体積は \(V\) であり、ばねは自然長であった。以下では、ピストンの移動やばねの伸縮は図の左右方向にのみ起こるものとする。また、はじめのピストンの左端の位置を原点とし、右向きを正の \(x\) 軸をとる。
はじめの状態から、シリンダー内の気体を加熱したところ、ピストンは \(+x\) 向きにゆっくりと動き、しばらくして、 \(x=V/S\) の石でピストンは静止した。
問1 シリンダー内の気体について、体積\(v\) \((V≦v≦2V)\)の状態における圧力\(p\)を、\(v\)の関数として表せ。 また、この関数が表すグラフを,\(V≦v≦2V\) の範囲いついて、\(p\) を縦軸、\(v\) を横軸にとって描け
問2 ピストンが動く間にシリンダー内の気体がした仕事を、 \(p_{0}\) ,\(V\) ,\(k\)、\(S\)を用いて表せ。
問3 シリンダー内の気体がした仕事は、一部は大気にした仕事と考えられ、残りは何らかの形のエネルギーに転化したと考えられる。このエネルギーの名称と、そのエネルギーの値を、\(x=V/S\)の位置でピストンが静止した状態について求めよ。
【問題PDF】
【解説】

【解説PDF】



コメント