統計について、何か書こう・・・
って思って、最初なので、何かなじみのあるもので書きたい・・・っておもって、
統計に関する記事の最初は、偏差値について。
偏差値って実はよく知らないのでは? って思ったりする。
まずは、ちょっと具体的な数値からはじめてみる。
こちらに2つのテスト結果がある。
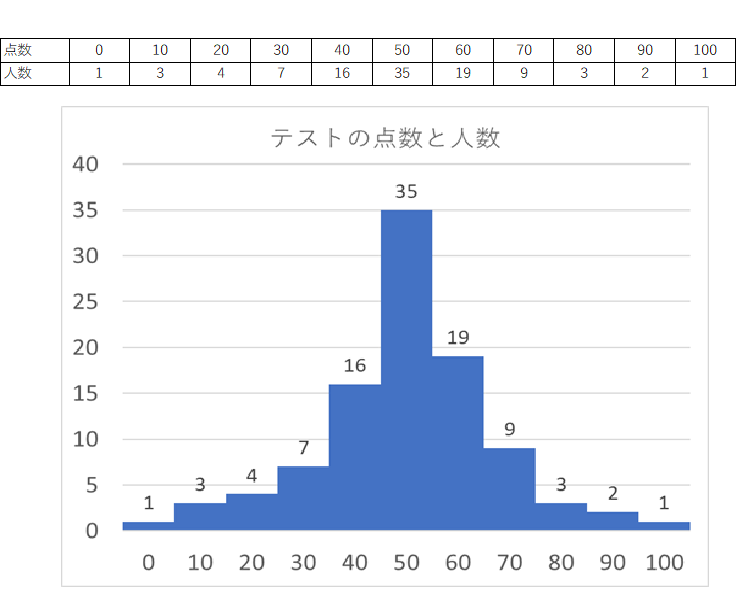
共にこのテストを受けた人数は100人で、平均点は両方とも50点である。
でも、グラフ(表とヒストグラム)を見てなんとなくわかるように、
【テスト結果1】では、平均点に集まっており、
【テスト結果2】では、0点から100点の間に人数がかなりばらつきがある。
でも・・・データ上では同じ平均点50点としてとらえられてしまう。
【テスト結果1】
【テスト結果2】
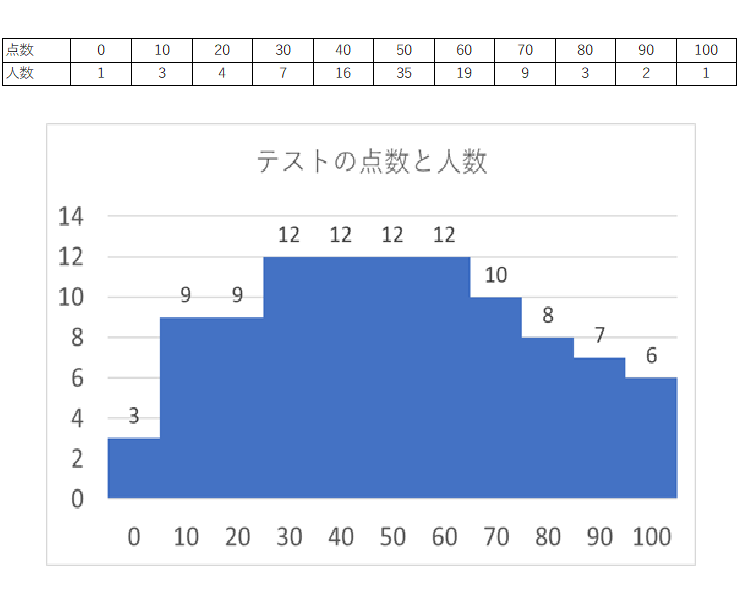
極論、平均点50点なので、50人が100点満点、50人が0点でも平均は50点になってしまう。
ここで、よく聞くのが、偏差値である。
例えば、テスト結果1において、90点取った時の偏差値はおよそ73であるのに対し、テスト結果2ではおよそ64である。テスト結果2で100点満点とっても偏差値は68ほどである。
偏差値って、特に高校・大学の入学試験や模試でよく使われる(他では確かに偏差値って使われないかなぁ~)んですが、偏差値ってそもそも

という式で表されており、ちょうど平均点は偏差値=50になる。
・・・・ってことは、そもそも生徒みんな高い点数を取るような学校だけでテストを受ければ、平均点が高いのでは?
・・・・っていうことは、その場合平均点を取れなかったら、偏差値50以下になる?
そう。偏差値を語る上では、テストを受ける人たちのレベルによって、偏差値は変わる!!
んである。
偏差値はあくまでも一つの指標だけであって・・・
と言いたいが、偏差値60!!って言った後に、いやぁ、実はこれは、○×テストで受けた偏差値で・・・なんか言おうものなら、こいつややこしいやつ・・・ってなるのである。
予備校などの模試の判定は、過去に受けた人の模試の結果や大学受験の合否情報がある(と思われる)ので、判定が出せているのでは?と想定している。
ひろゆきさん(だったかなぁ)がYouTubeで言ってたのは、
【世の中の半分は偏差値50以下なんですよ。】
って。 偏差値の式からみたら、ひろゆきさん(だったと思うが)の言ってたことは、ほぼほぼ正しいんですよね。で、偏差値の式でややこしいのが 標準偏差でして。
標準偏差を表す式は

で、その分散は、

と、これまた、ややこしい式になる。
これを「正規分布」で表すと、だいたいこのようになり、
偏差値50はちょうど中間、平均になるのですが、
偏差値60では、上位約16%。(100人いたら16番目くらい)
偏差値70では、上位約2.5%。 (100人いたら2~3番目くらい)
偏差値80ともなると、上位約0.14%となる。
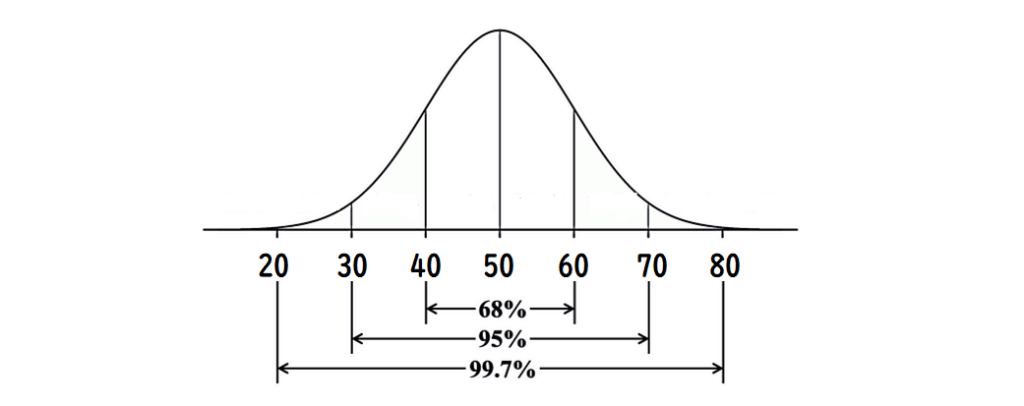
つまり、偏差値80とは、100人に一人もいなくて、1000人でやっと1人か2人。
という非常にレアな存在になるわけです。
具体的な数値であらわすと、現在の大学入学志願者をだいたい60万人とすると、偏差値50では30万人(平均なので)、
偏差値60は、上位約9.6万人、
偏差値70ではだいたい1万5千人、
偏差値80を超えるのは全大学志願者の中で、たったの900人程度になります。
ちなみに...
偏差値90は上位0.003%なので、 約20人。
偏差値100は上位0.0000099%なので、一人にも満たず、0.05人となります。
これは、大学受験志願者全体を母集団の人数(60万人)とし、正規分布にて試算しているので、ハイレベルな模試になれはなるほど、平均点が上がり、偏差値は低くなるかもしれないけど、その分問題も難しくなるので、ハイレベルなメンバー間で偏差値が良かったら、更に自信がつくかもね。
これから、時間が空いたときには、こんな感じで統計やデータに関する記事をより具体的な感じで書こうかなっておもってます。



コメント