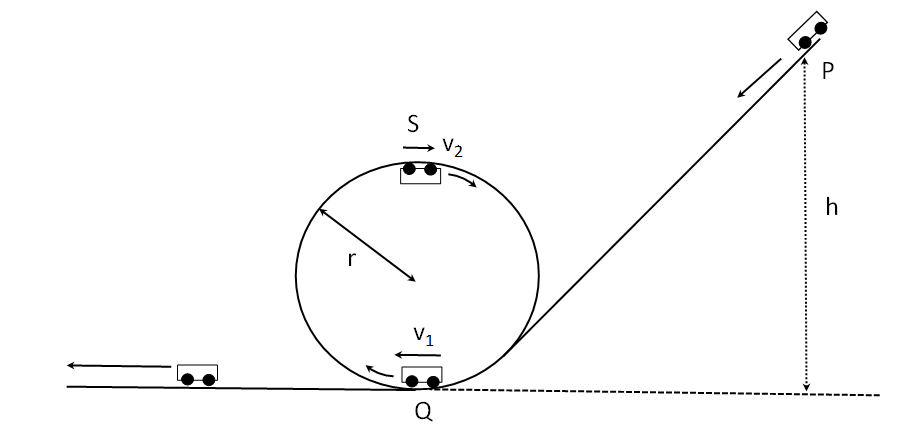
図のように、質量 \(m\)〔kg〕の台車が、地上からの高さ \(h\)〔m〕の点 P から静かに動きはじめ、なめらかな斜面をすべり降り、半径 \(r\)〔m〕のなめらかな円形のループに入り、これを1回転して通過し、地上平面に点Qで接する。重力加速度の大きさを \(g\)〔m/s2〕として、以下の各問に答えよ
問1 地面を基準面としたときの点 Pでの台車の位置エネルギーを求めよ。
問2 最初に点 Q を通るとき、加速度はどの方向を向いているか。
問3 そのときの速さは \(v_{1}\)〔m/s2〕であった。加速度の大きさを求めよ
問4 そのとき、台車が受ける垂直抗力の大きさを求めよ。
問5 ループの最上点 S での台車の速さ \(v_{2}\) 〔m/s〕を \(h\) , \(g\),\(r\) を用いて示せ
問6 台車がループの最上点 S を、落下せず無事に通過するために必要な \(h\) の最小の値を求めよ。
(広島工業大学)
【問題PDF】
【解説】




コメント