【問題】
■自動車の加速度による位置・時間を求める問題。
■加速度のグラフを読み解く問題
ここに長い直線道路があるとする。この道路上に \(x\)軸をとり、時刻 \(t\)〔s〕=0〔s〕で \(x\)軸の原点に自動車Aが停車していたとする。 このとき、Aの前方(\(x\)の正方向)20〔m〕を自動車Bが速さ24〔m/s〕で遠ざかっていった。その後の自動車A,Bの加速度と \(t\)〔s〕の関係は下のグラフのようになった。
時刻 \(t\)〔s〕の時のA,Bの位置をそれぞれ、\(x_{A}\)〔m〕、\(x_{B}\)〔m〕として、各問いに答えよ。
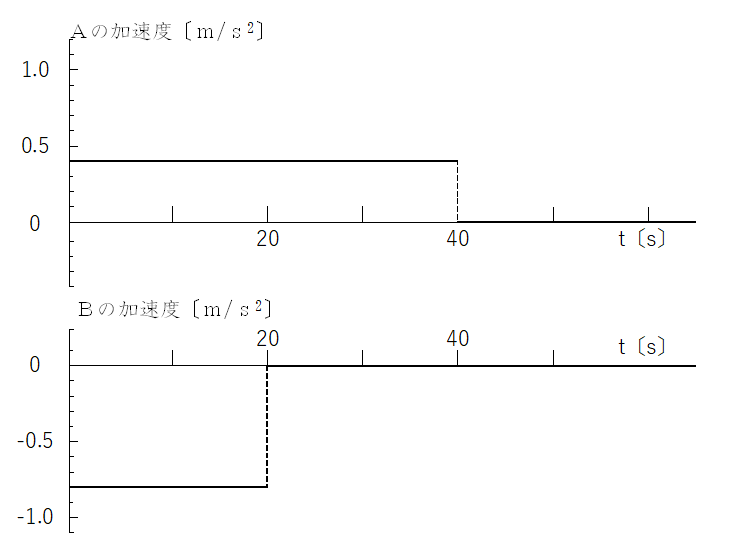
問1 A,Bの速さと時刻 \(t\)〔s〕の関係をグラフにしなさい。
(ただし、横軸を時刻〔s〕、縦軸を速度〔m/s〕と置くこと。)
問2 \(t\)〔s〕≧40sのとき、\(x_{A}\)〔m〕、\(x_{B}\)〔m〕を \(t\)で表せ
問3 AがBに追いつく時刻 \(t_{m}\)〔s〕の値を求めよ
【問題PDF】
【解説】


【解説PDF】



コメント