【問題】
空欄の(ア)~(カ)に当てはまる式を求めよ。
また、空欄(a)~(e)に当てはまる語句
を解答群から選べ。 図のように長さ \(l\) 〔m〕,幅 \(d\)〔m〕,高さ \(h\) 〔m〕の直方体の胴体の各辺に沿って,\(x\) 軸、\(y\) 軸,\(z\) 軸をとる。

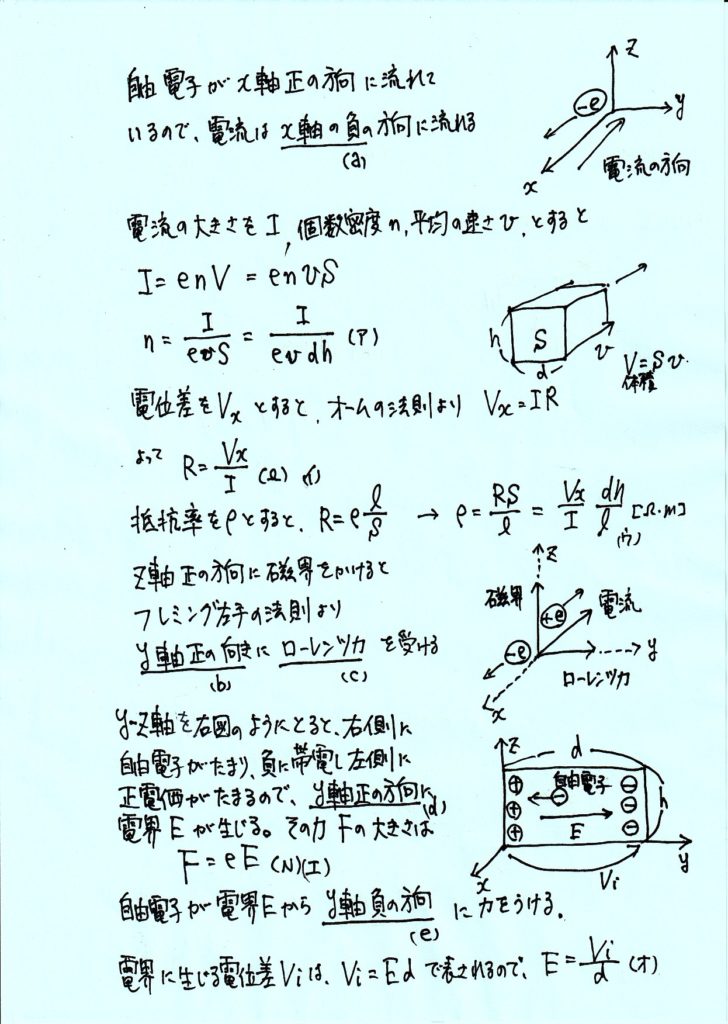
電荷-\(e\) 〔C〕の自由電子が導体内を一様に \(x\)軸の正の向きに運動するとき、導体中には【 a 】の向きに電流が流れる。 電流の大きさが \(I\)〔A〕であるとき、自由電子の平均の速さを \(v\)〔m/s〕とすると、自由電子の単位体積あたりの個数は【 ア 】〔個/m3〕である。また、導体の 方向の両端の電位差を \(V\)x 〔V〕とすると、導体電堆の抵抗値は【 イ 】〔Ω〕と表され、導体の抵抗率は【 ウ 】〔Ω・m〕と表される。
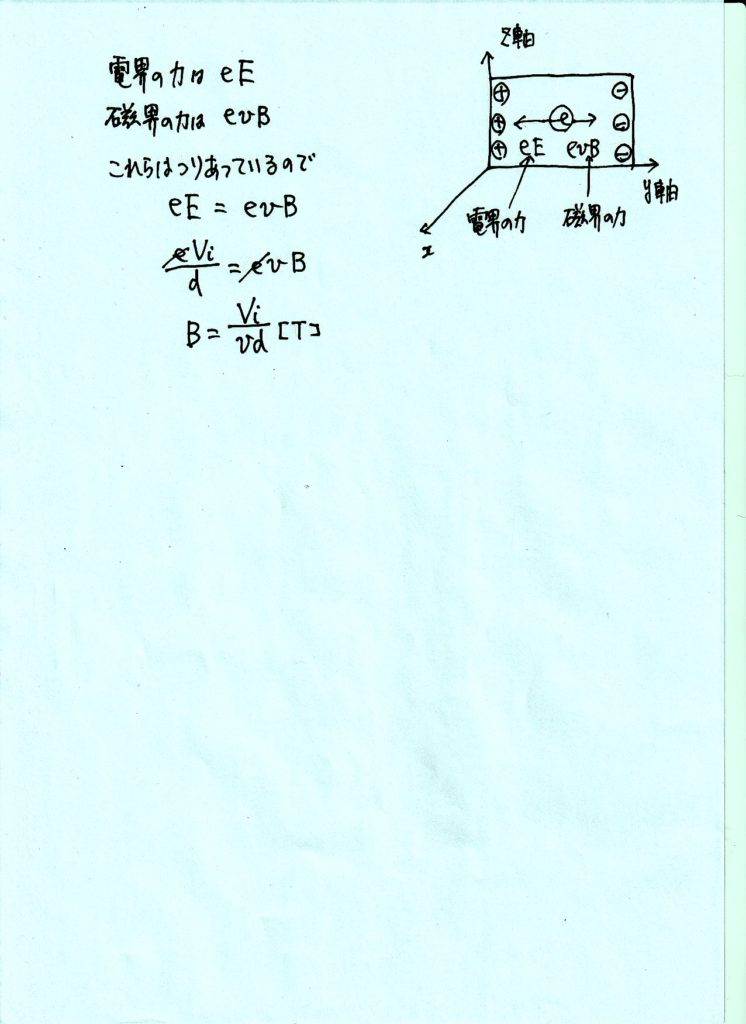
\(z\)軸の正の向きに一様な磁界を加えると、 \(x\)軸の正の向きに運動する自由電子は【 b 】の向きに【 c 】力を受ける。 この力によって自由電子の一部は導体の一端面に集まり、この面は負に帯電する。また、逆側の端面では電子が少なくなって正に帯電する。この結果、導体中には【 d 】の向きに大きさ \(E\)〔V/m〕の電界が生じ、自由電子はこの電界から大きさ【 エ 】〔N〕の力を【 e 】の向きに受ける。 この電界から受ける力と磁界から受ける力がつりあうことにより、自由電子は導体中に直進する。
このように磁界を加えたときに導体中に発生する電界の大きさ は、電界により生じる両端間の電位差 \(V_{i}\)i〔V〕を測定することによって、 \(E\) =【 オ 】〔V/m〕と計算される。また、導体中の時速密度の大きさは、\(V_{i}\),\(v\) , \(d\) を用いて【 カ 】〔T〕と求められる。したがって導体の大きさ、自由電子の単位体積あたりの個数、および抵抗率が分かっていれば、 と の比から磁束密度の大きさを測定することが出来る。
〔解答群〕
(1)\(x\) 軸の正(2)\(x\) 軸の負(3)\(y\) 軸の正(4)\(y\) 軸の負(5) \(z\) 軸の正
(6)\(z\) 軸の負(7)ヘンリー(8)クーロン(9)ローレンツ(10)フレミング
【問題PDF】
【解説】
【解説PDF】


コメント