2．電磁気学　16．RLC交流回路　直列・並列　 難易度★☆☆☆☆

｛　｝の中の（1）～（4）の中で正しいものを選びなさい。

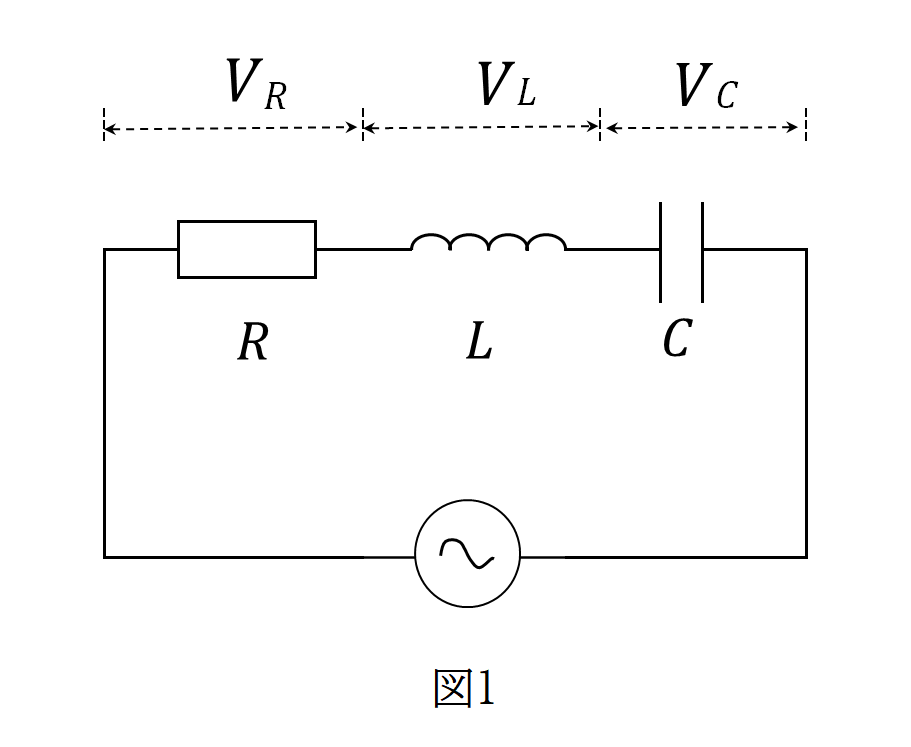
図1の回路において、抵抗、コイル、コンデンサのリアクタンスをそれぞれ、\(R\)   ，\(L\)  ，\(C\)  　とおくと、流れる電流が共通なので、 \(I\) ＝\(I\)₀ \(\sin ωt\)     と置くと、

\(V\)_R ＝｛ （1）\(RI\)₀ \(\sin ωt\)  （2）\(RI\)₀ \(\cos ωt\)    （3）－\(RI\)₀ \(\cos ωt\)     （4）－ \(RI\)₀ \(\sin ωt\)    }

\(V\)_L ＝｛（1）\(ωLI\)₀ \(\sin ωt\)    （2） \(ωLI\)₀ \(\cos ωt\)  （3）－\(ωLI\)₀ \(\cos ωt\)   （4）－\(ωLI\)₀ \(\sin ωt\)  }

\(V\)_C ＝ ｛（1） \(\displaystyle\frac{I_{o}}{\omega C}\) \(\sin ωt\)     （2） \(\displaystyle\frac{I_{o}}{\omega C}\) \(\cos ωt\)   （3）－ \(\displaystyle\frac{I_{o}}{\omega C}\) \(\cos ωt\)     （4）－  \(\displaystyle\frac{I_{o}}{\omega C}\) \(\sin ωt\)   }

とおける。

————————————————————————————————————–

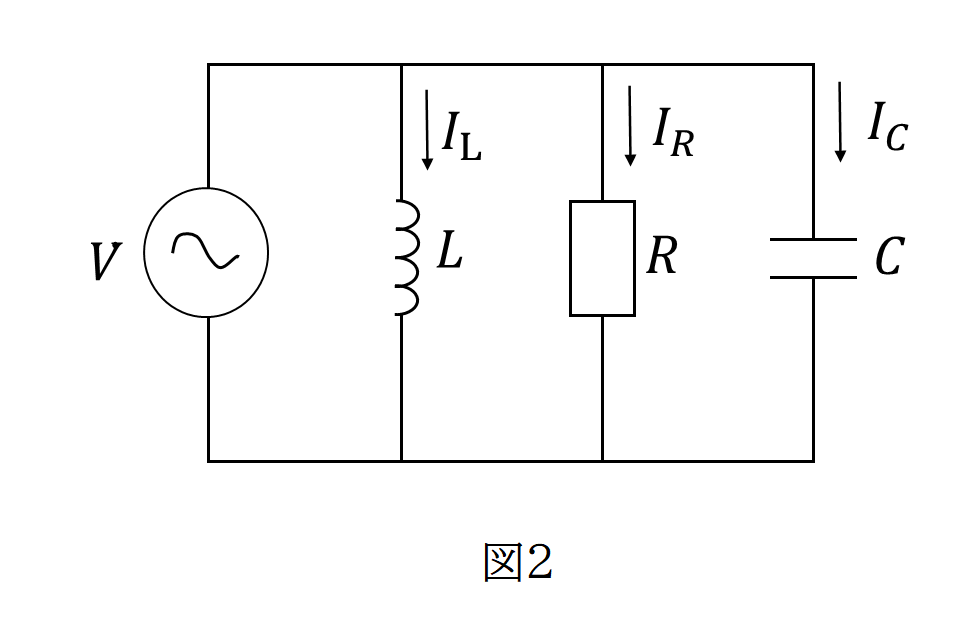
図2の回路において、抵抗、コイル、コンデンサのリアクタンスをそれぞれ、 \(R\)   ，\(L\)  ，\(C\) とおくと電源電圧が共通なので、\(V\)  ＝ \(V\)₀ \(\sin ωt\)  と置くと、

\(I\)_R ＝｛（1） \(\displaystyle\frac{V_{o}}{R}\) \(\sin ωt\)     （2） \(\displaystyle\frac{V_{o}}{R}\) \(\cos ωt\)   （3）－ \(\displaystyle\frac{V_{o}}{R}\) \(\cos ωt\)     （4）－  \(\displaystyle\frac{V_{o}}{R}\) \(\sin ωt\)   }

\(I\)_L ＝｛（1） \(\displaystyle\frac{I_{o}}{\omega L}\) \(\sin ωt\)     （2） \(\displaystyle\frac{I_{o}}{\omega L}\) \(\cos ωt\)   （3）－ \(\displaystyle\frac{I_{o}}{\omega L}\) \(\cos ωt\)     （4）－  \(\displaystyle\frac{I_{o}}{\omega L}\) \(\sin ωt\)   }

\(I\)_C ＝｛ （1） \(\omega CV\)₀ \(\sin ωt\)     （2） \(\omega CV\)₀ \(\cos ωt\)   （3）－\(\omega CV\)₀ \(\cos ωt\)     （4）－  \(\omega CV\)₀ \(\sin ωt\)   }

---

【問題PDF】

---

【解説】

---

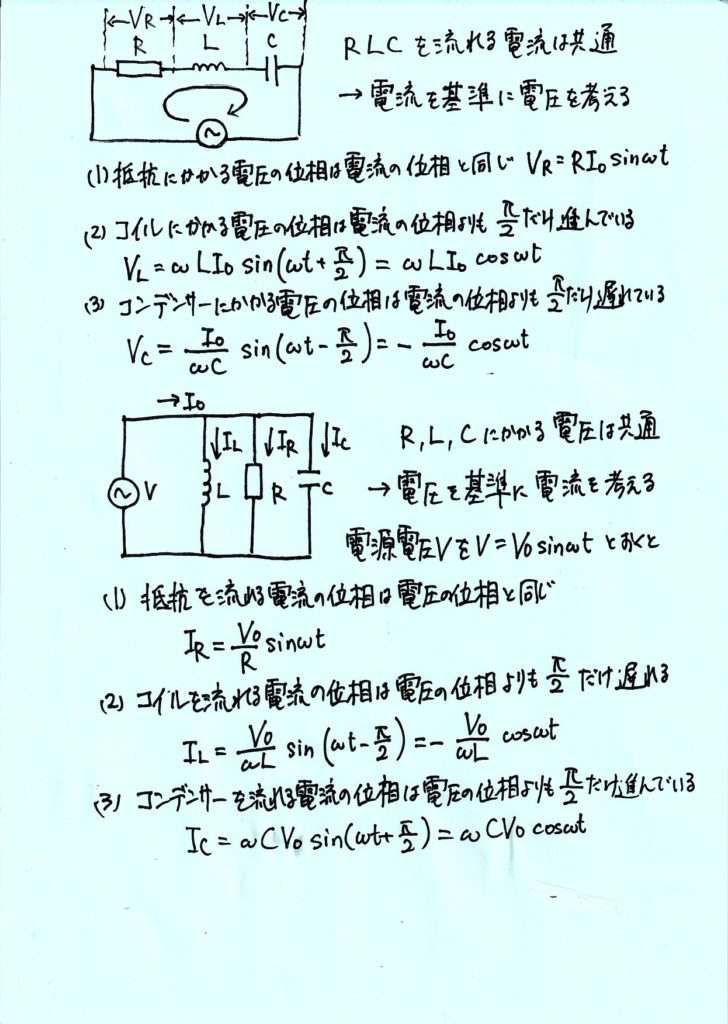
【解説PDF】