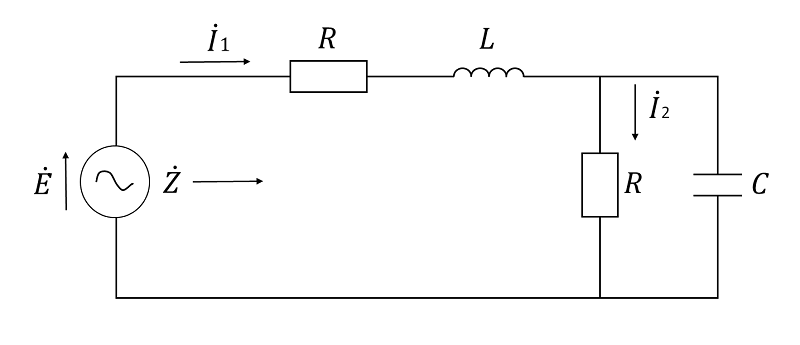
次の文章は, RLC 正弦波交流回路に関する記述である。文中の【 】に当てはまるものを解答群の中から選びなさい。
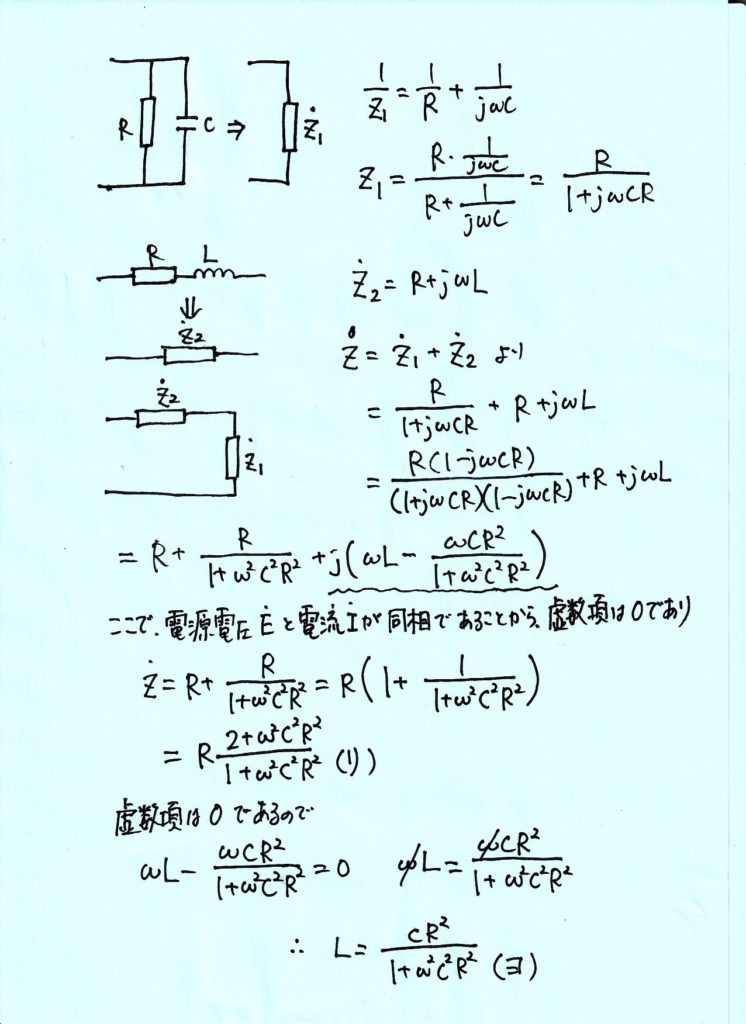
図に示す RLC 回路を考える。正弦波交流電圧 \(\dot E \) の角周波数は ω(ω>0) とする。いま,電源電圧 \(\dot E \) と電流 \(\dot I \)1 が同相であるとする。このとき,電源電圧 \(\dot E \) からみた回路のインピーダンスを \(\dot Z \) とおくと,\(\dot Z \) は純抵抗となり,\(\dot Z \) = 【 1 】となる。また,インダクタンス \(L\) は \(L\) = 【 2 】 となる。
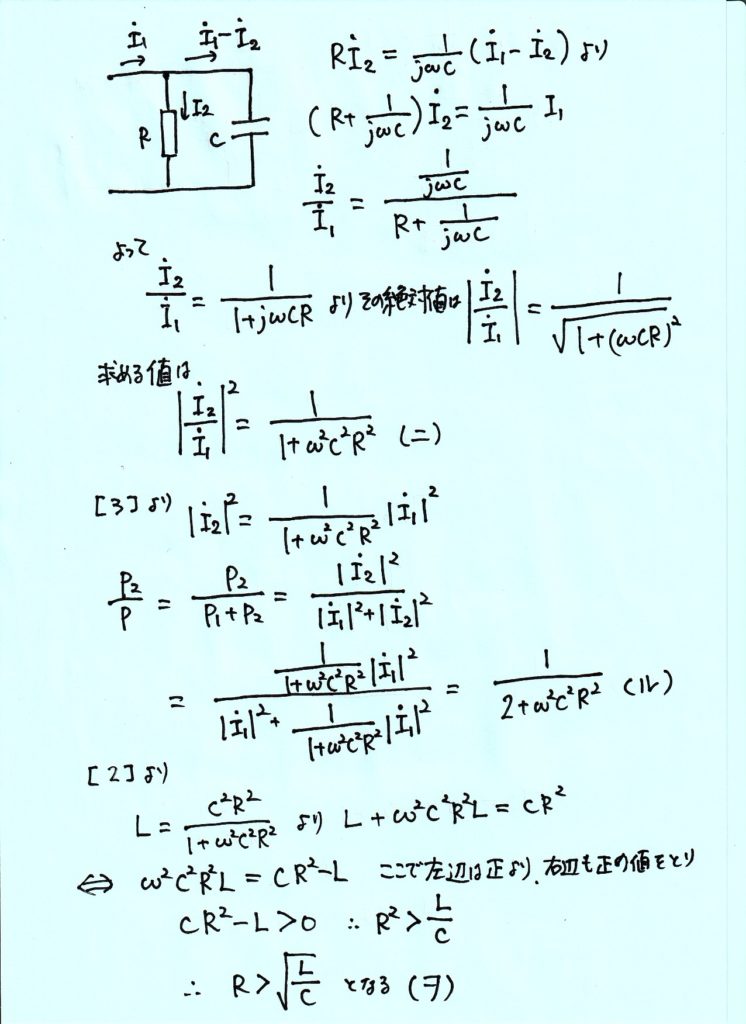
電流の分流比に着目すると,\(\dot I \)1 と \(\dot I \)2 について, \(\displaystyle \left| \frac {{\dot I}_{2}}{{\dot I}_{1}}\right| ^{2} \)=【 3 】となる。 \(\dot I \)1 が流れる抵抗 \(R\) の消費電力を \(\dot P \)1 , \(\dot I \)2 が流れる抵抗 \(R\) の消費電力を \(\dot P \)2 とする。電圧源が RLC 回路に供給する電力を \(\dot P \) とおくと, \(\dot P \) =\(\dot P \)1 + \(\dot P \)2 となり, \(\displaystyle\frac{P_{2}}{P}\) = 【 4 】となる。
この回路では,電源電圧 \(\dot E \) と電流 \(\dot I \)1 が同相であることから \(R\) と \(\sqrt{LC}\) の大小関係は常に【 5 】となる。
【解答群】
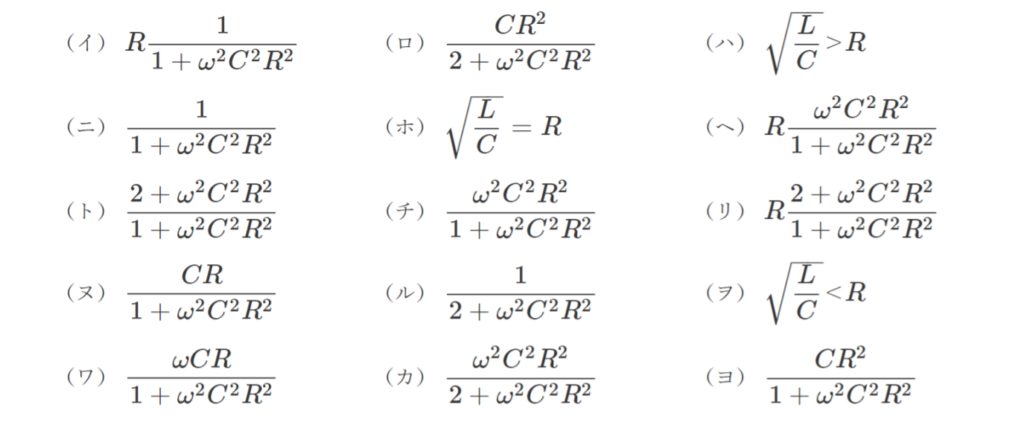
(2012(H24)電験2種 理論問題)
【問題PDF】
【解説】
【解説PDF】


コメント