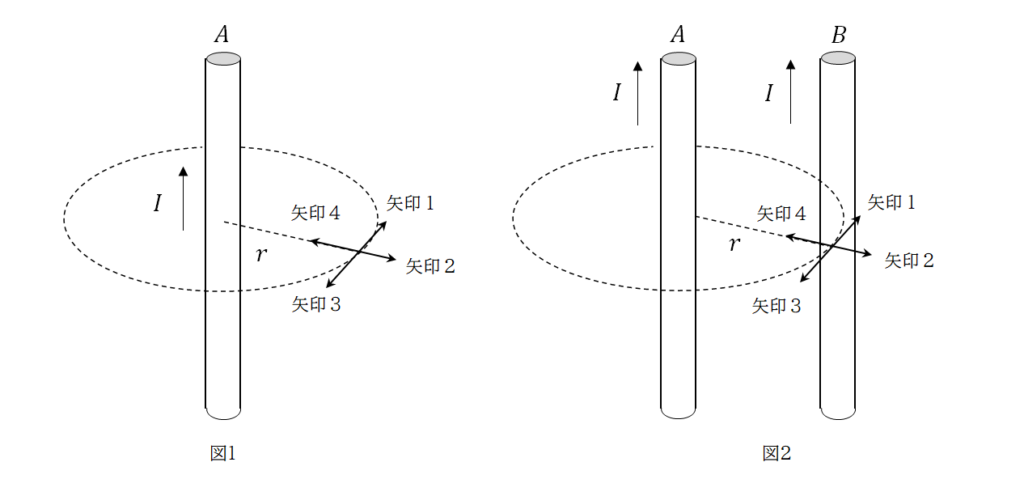
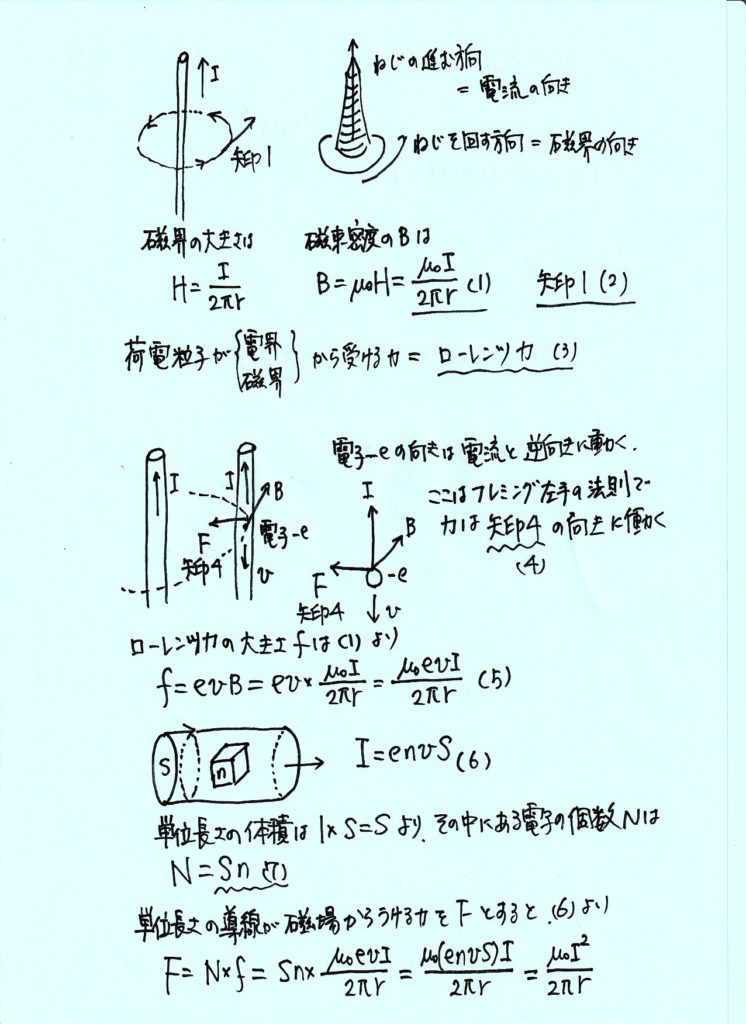
電流は周りの空間に磁場を作る。図1のように、真空中に置かれた無限に長い直線導線Aに矢印の向きに強さ\(I\)の電流を流すと、導線Aの中心から距離 \(r\) だけ離れた位置Pにできる磁場の磁束密度の大きさは真空の透磁率を\(μ\)0として、【 1 】であり、向きは【 2 】の向きである。
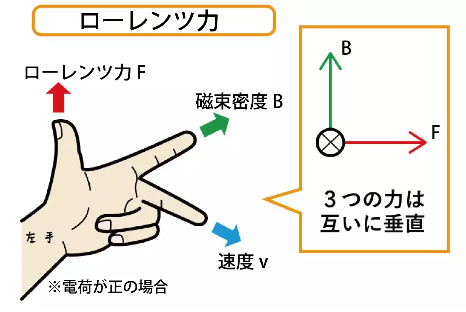
次に図2のように、位置Pに細い導線Bを導線Aと間隔\(r\)で平行に置き、導線Aを流れる電流と同じ向きで同じ強さの電流を流した。導線Bの中で動く自由電子(以後、電子と呼ぶ)には、導線Aが作る磁場によって、【 3 】とよばれる力が働く。電子の電気量をー\(e\)とすると、この導線Bの中を平均の速度\(v\)で動く電子には,【 4 】の向きに大きさ【 5 】の力が働く。
ここで、導線Bの断面積を \(S\) とし、導線内での電子の単位あたりの個数\(n\)とすると、電流の強さ \(I\) と電子の速さvの間には、\(I\) =【 6 】の関係がある。また、単位長さの導線内には、【 7 】個の電子が存在するので、単位長さの導線が磁場から受ける力は、\(n\) や \(S\) を用いずに、【 8 】と表すことができる。
(関西大)
【問題PDF】
【解説】
【解説PDF】


コメント