端子a,b,c,dをもつ基板上に、2個の抵抗器 \(R_{1}\),\(R_{2}\) 1個のコイル \(L\),1個のコンデンサー\(C\)が取り付けられているが、配線を見ることができない。そこで、次のような測定を行い、各部品の間がどのように配線されているか調べた。
【 測定I 】
端子間に直流電流を流して抵抗を測定したところ、ab間の抵抗は600Ωであった。また、ab間を短絡した状態では、ac間の抵抗は150Ωであった。
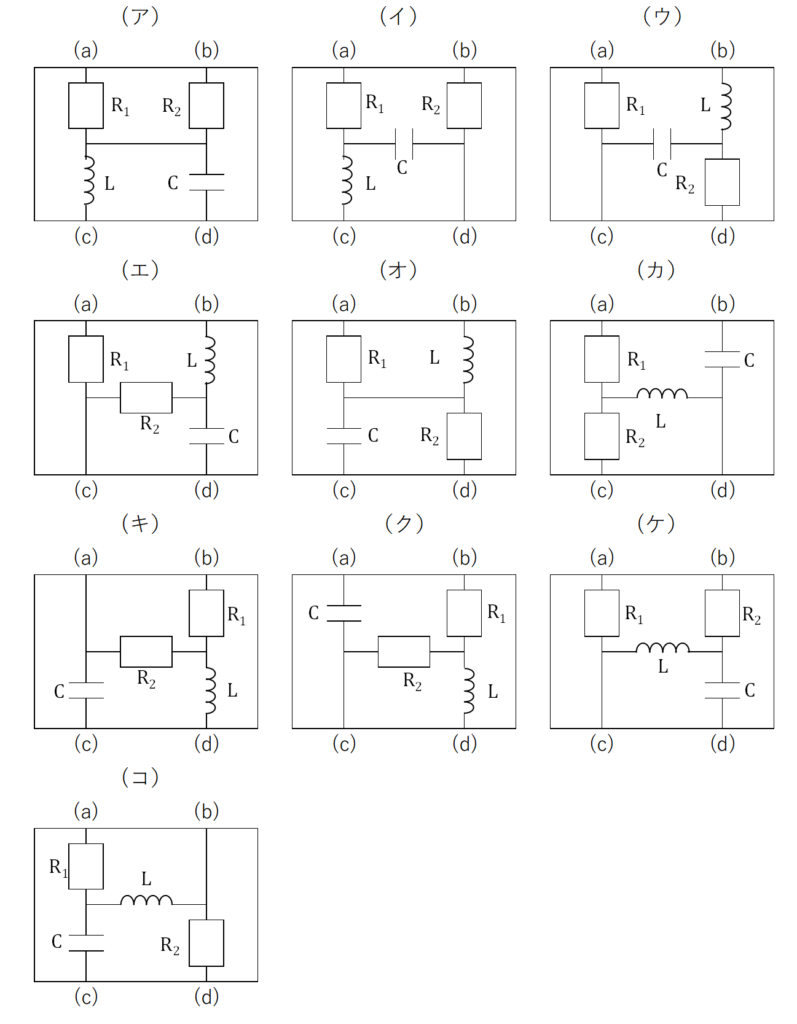
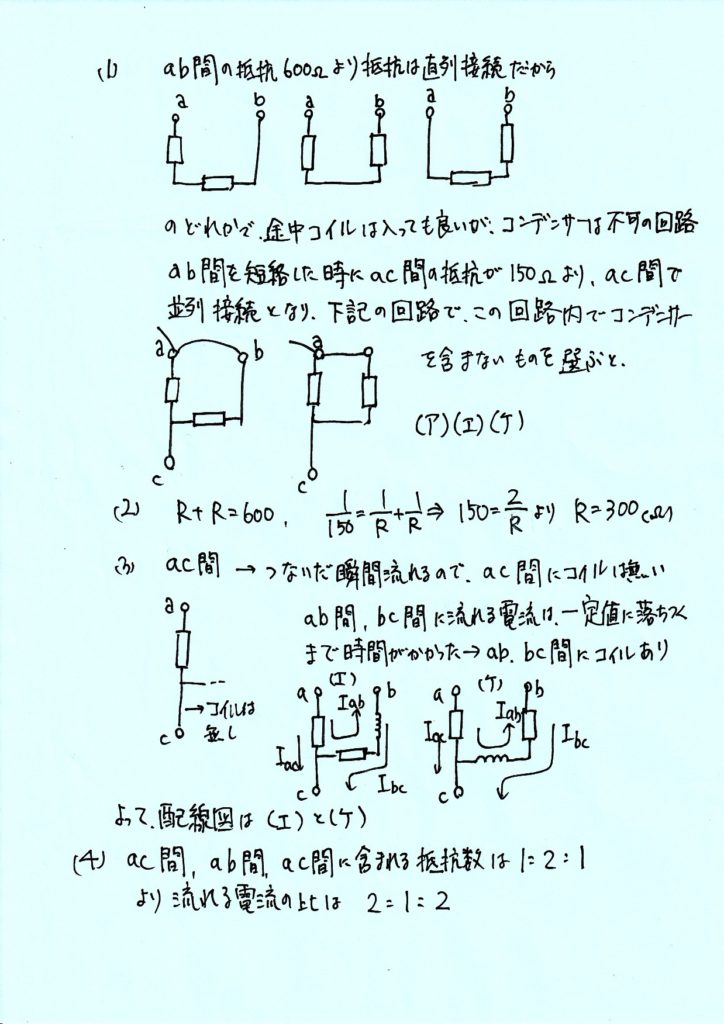
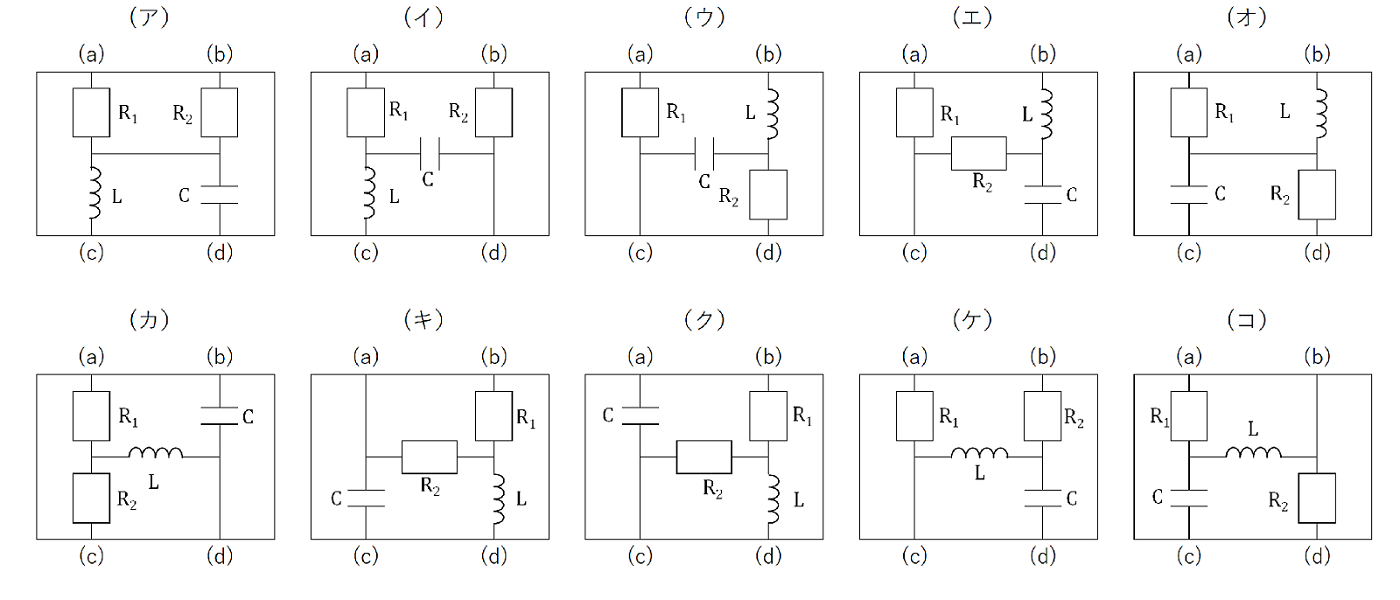
(1)この測定I から考えられる配線を、文末の配線図(ア)~(コ)のうちから選べ。複数ある場合は、すべての記号を記せ。
(2)(1)で選んだ配線図に基づいて、\(R_{1}\),\(R_{2}\)の抵抗値を求めよ。解答に複数の可能性がある場合は、そのうち1つについて求めればよい。
【 測定Ⅱ 】
適当な2端子間に電池をつないだ直後にその回路に流れる電流の時間変化を即例したところ、ac間では電池をつないだ瞬間に一定の電流が流れたのに対して、ab間とbc間では0から増大して一定値に達するまでに時間がかかった。 また、一定値に落ち着いたときの電流値は、それぞれ、\(I_{ac}\),\(I_{ab}\),\(I_{bc}\) であった。
(3)測定Iと測定Ⅱの結果から考えられる配線を、文末の配線図(ア)~(コ)のうちから選べ。複数ある場合は、すべての記号を記せ。
(4)(3)で選んだ配線図に基づいて \(I_{ac}\),\(I_{ab}\),\(I_{bc}\) の比を求めよ。ただし、つないだ電池の起電力は等しく、内部抵抗は無視できるとする。解答に複数の可能性がある場合は、そのうちの 1つについて求めればよい。
【 測定Ⅲ 】
bd間に電池をつないで十分時間が経った後、電池をはずし、cd間をつないだ、このとき、ab間の電圧をオシロスコープで観測すると、振動数200Hzの振動が見られた。
(5)上記の全測定から考えられる配線を、文末の配線図(ア)~(コ)のうちから1つ選び、その記号を記せ。
【 測定Ⅳ 】
bd間の交流に対する抵抗(インピーダンス)Zを測定したところ、\(Z\)=500Ωであった。このとき、用いた交流の周波数は100Hzであった。
(6)測定Ⅲ、ⅣからコイルLの自己インダクタンスとコンデンサーCの電気容量を求めたい。次の( イ )~( へ )に適当な語句または数値を入れよ。
抵抗器と墾田だーを直列につないだ回路に交流を流す場合を考える。このとき、コイルでは、( イ )に対する( ロ )の( ハ )が\(π\)/2だけ遅れ、逆にコンデンサーでは\(π\)/2だけ進むために、この回路の交流に対する抵抗(インピーダンス)\(Z\)は、単純に抵抗器の抵抗とコイルやコンデンサーの( ニ )の和とならず、
\(\begin{eqnarray} Z = \sqrt{R^{2}+\left(\omega L – \frac{1}{\omega C}\right) ^{2}} \\[ 5pt ]\end{eqnarray}\)
となる。ただし、\(R\)は抵抗器の抵抗、\(L\)はコイルの自己のインダクタンス、\(C\) はコンデンサーの電気容量、ωは測定に用いた交流の角周波数を示す。
(5)で選んだ配線図に基づいて計算すると、コイル \(L\) の自己インダクタンスは( ホ )、コンデンサー \(C\) の電気容量は( へ )と計算される。
(関学大)
【問題PDF】
【解説】

【解説PDF】



コメント