次の文章は,影像(鏡像)電荷を用いた静電界解析に関する記述である。文中の【 】に当てはまる最も適切なものを解答群の中から選べ。なお,電位は無限遠点を基準とする。
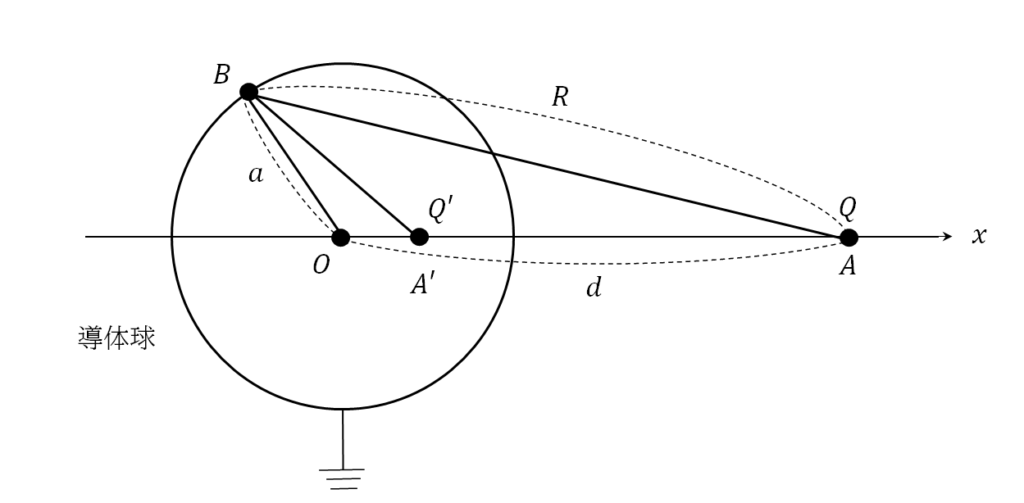
誘電率 ε0 の真空中に半径\(a\) の接地された導体球が存在する。図のように,導体球の中心が原点 O となるように \(x\) 軸を定め, \(x\) 軸上の \(x\)=\(d\) の点 A に電荷 \(Q\) の点電荷を置く(ただし \(d\)>\(a\) である)。このとき導体球が真空中に作り出す電界を影像電荷によって表現しよう。
導体球は接地されているので,導体球の表面のあらゆる点で電位が零になるという境界条件を満たす必要がある。そこで,図に示す導体球表面の点 B で境界条件を満たすように,導体球の代わりにその内部の \(x\) 軸上の点 \(A\)′ に影像電荷 \(Q\)′ を置く。
まず,点 \(A\)′ の \(x\) 座標を \(x\)=【 1 】とすると, △AOB と △BOA′ が相似となる。辺 AB の長さを \(R\) とすると,点 A の点電荷が点 B に作り出す電位は【 2 】となるので, \(Q\)′=【 3 】とすることによって,点 B で境界条件が満たされる。相似条件は導体球表面の任意の点について成立するので,点電荷と影像電荷によって導体球表面のあらゆる点で境界条件を満たすことができ,影像電荷が真空領域に作り出す電界は,導体球が作る電界と一致する。ガウスの法則から,点電荷によって導体球に誘起された電荷の総量は,影像電荷と同じ \(Q\)′ となる。
さらに \(x\)=−\(d\) の点に電荷 −\(Q\) の点電荷を置く場合には, \(x\)=【 4 】の地点に影像電荷を追加することによって,真空中の電界を表現することができる。このとき,二つの点電荷によって導体球に誘起される総電荷は【 5 】となる。
【問題PDF】
【解説】

【解説PDF】
点電荷と導体が作る電場において、そのまま計算すると非常に難しいことがある。その際に、仮想的に鏡の位置に反対の電荷を置くことにより、非常に想像・計算がし易くなるのですが・・・・
そこにたどり着くまでが・・・判らないという方が多いと思われるので、その時は、今回の問題ではなく、もっと簡単な鏡像問題から手をつけることをお勧めします。


コメント