図1のように、水平床面で一端を固定したばね(ばね定数 \(k\))の他端に物体 \(M\)(質量 \(m\))を取り付ける。
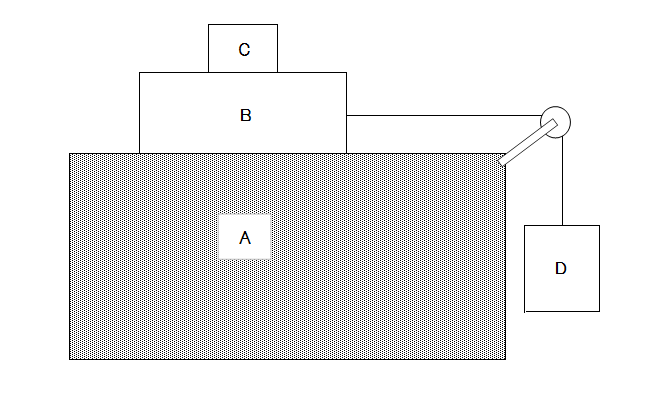
図1
物体\(M\)とばねの運動方向は図の\(x\)軸方向にかぎられ、物体\(M\)の位置を座標\(x\)で表す。ばねが自然長の状態にあるとき\(x\) = 0 とし、伸びる向きに\(x\) の正の向きを定める。物体と床面との間には摩擦が働くものとして次のような振動実験を行う。
まず、物体\(M\)を\(x\)の位置まで引っ張って静かに手放すことを、\(x\)の値を繰り返し、\(x\)がある値 \(d\)より小さいときには物体は動かず、\(d\)よりも大きいときにはすべり出すことを確かめた。
次に、物体を位置 \(x_{0}\) >\(d\)まで引っ張って静かに手放し、その瞬間からの時間を\(t\)として物体の動きを観察した。 物体ははじめ次第に速さを増し、最大の速さに達した後、減速して、速さが 0となった。 そのときの位置は\(x_{1}\)<0であった。
その後、物体は再び逆向きに動きだし、何回かの折り返しを繰り返した後、ついに\(n\) 回目の折り返し点\(x_{n}\)で停止した。このとき、以下の設問に答えよ。結果だけでなく、考え方や途中の計算も簡単に示せ。 ただし、重力加速度は\(g\)で表し、ばねの質量や空気抵抗は無視しうるものとする。
(1)物体\(M\)と床面との間の静止摩擦係数\(μ_{0}\) と運動摩擦係数\(μ\) を求めよ。
(2)位置\(x_{1}\)で速さが0となった時間\(t_{1}\)を求めよ。
(3)はじめて速さが最大に達したときの位置\(a\)とその時間\(t_{a}\)を求めよ。
(4)最後に位置\(x_{n}\) で停止するまでに物体が運動した全行程の長さ\(L\) と\(x_{n}\)との関係を求めよ。
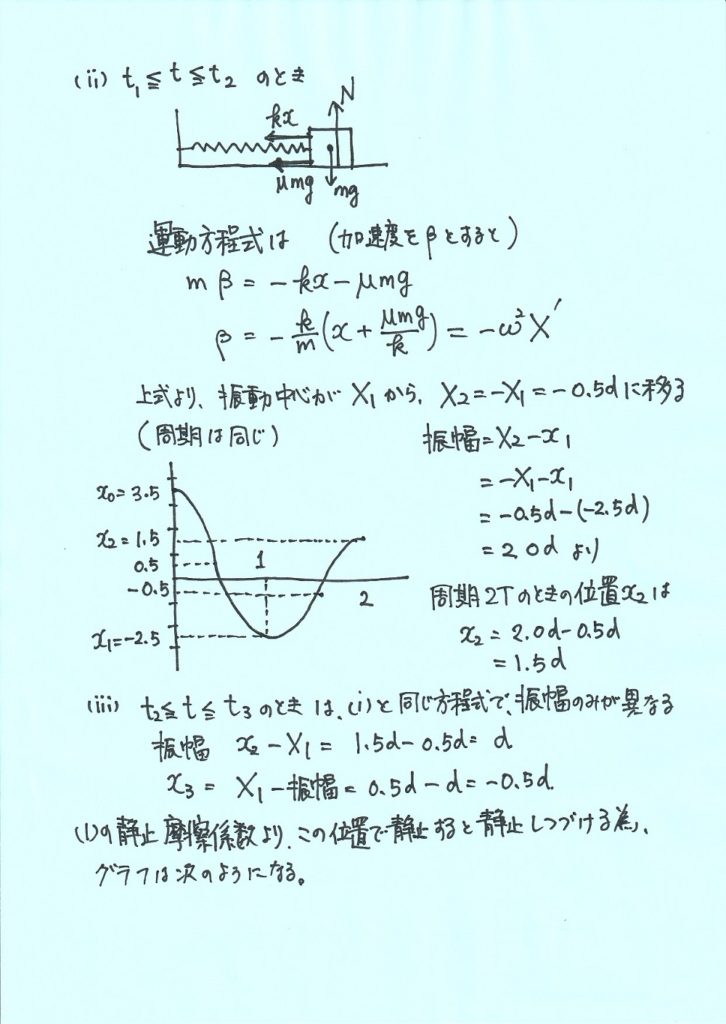
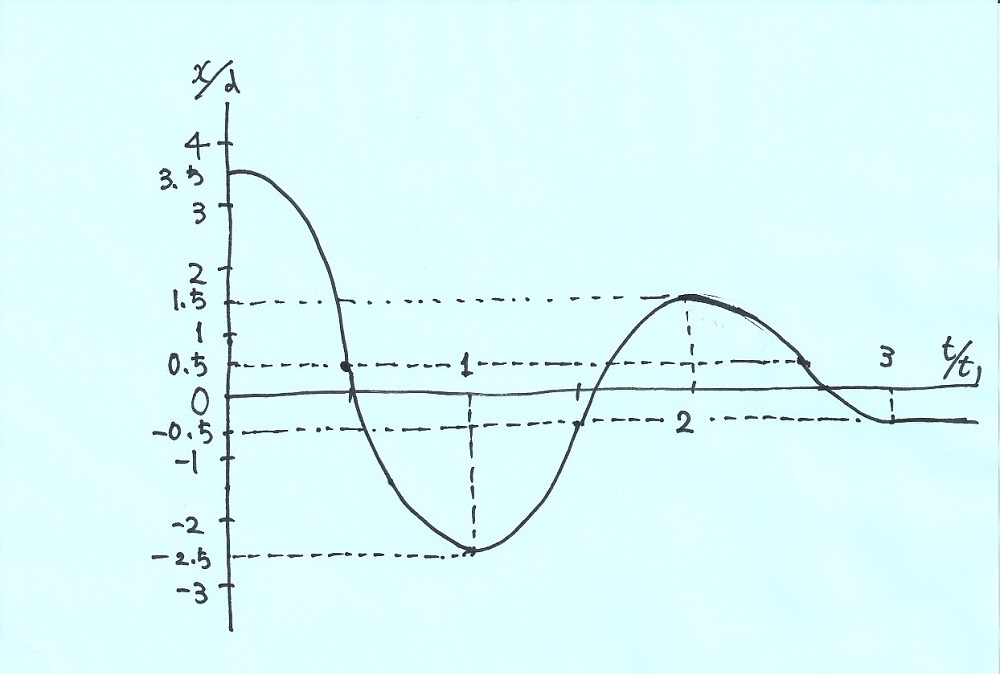
(5)物体\(M\)の位置\(x\) と時間\(t\) との関係を図2に示すようなグラフに図示せよ。ただし、この設問においては\(x_{0}\)=3.5\(d\)、\(x_{1}\)=-2.5\(d\)とする。
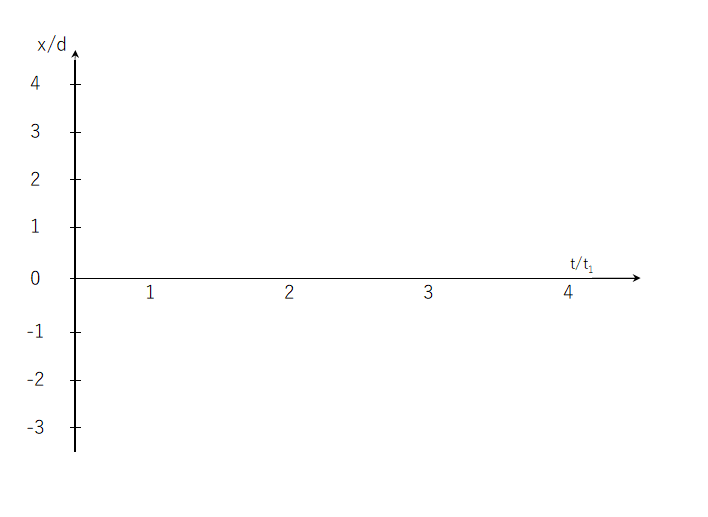
図2
(東京大)
【問題文PDF】
【解説】
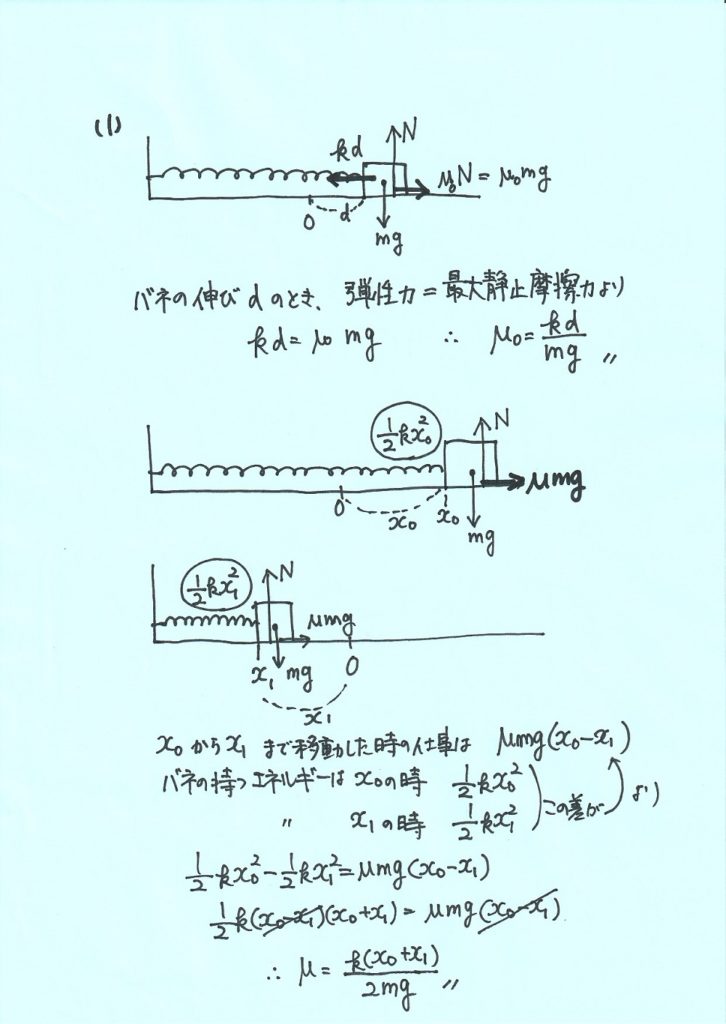
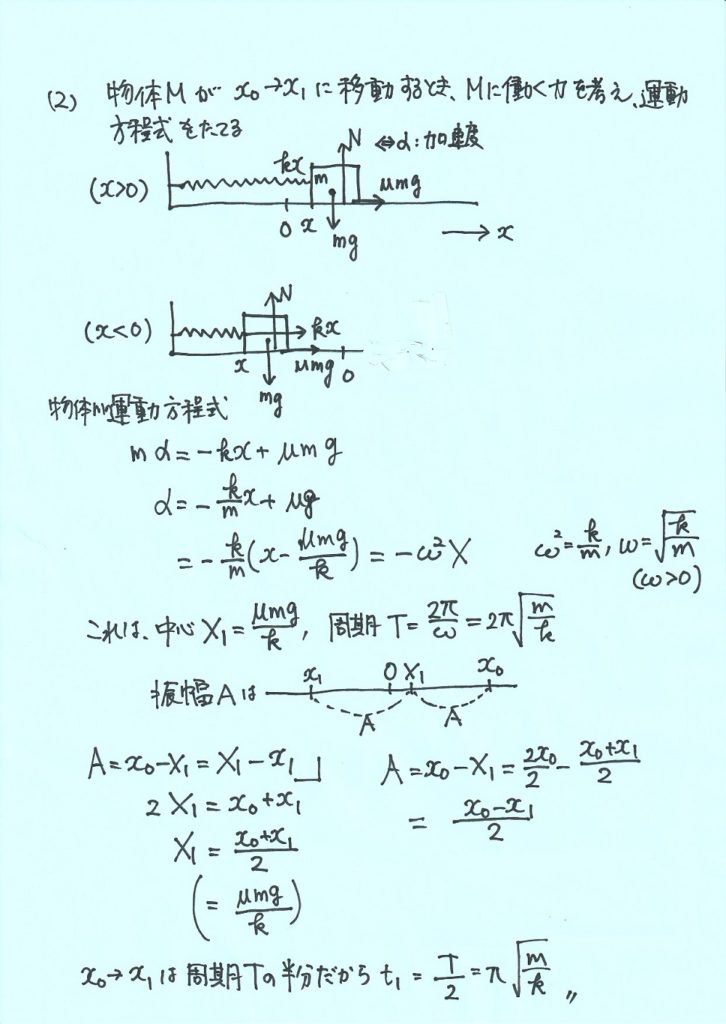

【解説PDF】



コメント