ある日の午前中に雪が降り始めた。
除雪車が正午に除雪をし始め、1時間で2マイルの除雪をし、さらに次の1時間で1マイルの除雪を完了した。雪の降り始めた時刻は午前何時何分??
但し、雪は常に一定のペースで積もり、除雪車は時間あたり一定量の除雪をするものとする。
【問題文PDF】
【解説】
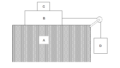
\( \fbox { イメージ } \)
問題文より、除雪車が通り始める正午、1時間後、2時間後のイメージは以下のようになります。
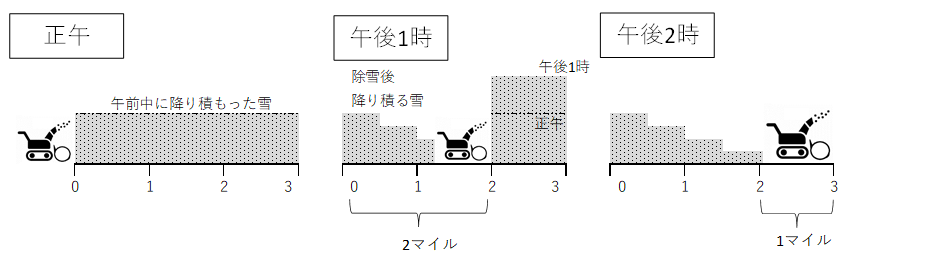
\( \fbox { 要点 } \)
(1)除雪車の単位あたりの作業量が一定
⇒ 除雪車の速度 \(v(t)\) ✕ 作業する積雪量 \(h(t)\) = 一定(const.)
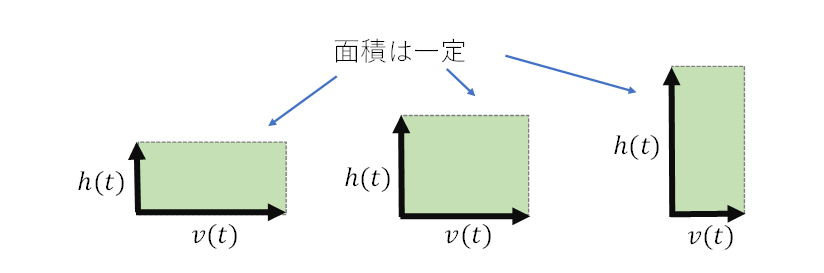
積雪が少ないと早く作業できるが ⇒⇒⇒⇒⇒ 積雪が多いとゆっくりとした作業になる
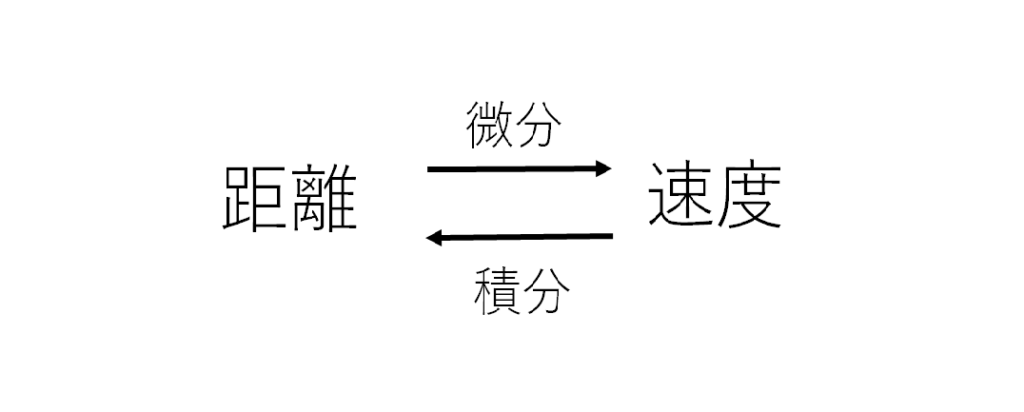
(2)速度を時間で積分すると、距離になる。
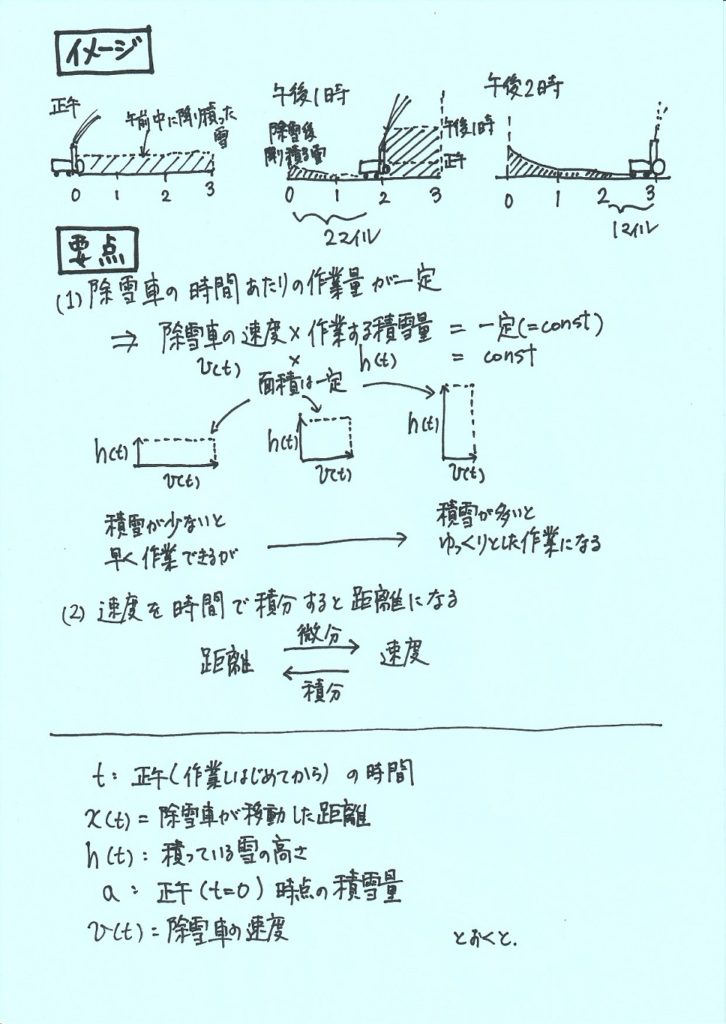
\(t\):正午(作業しはじめて)からの時間
\(x(t)\):除雪車が移動した距離
\(h(t)\):積もっている雪の高さ
\(a\):正午(\(t=0)\) 時点の積雪量
\(v(t)\):除雪車の速度
とおくと、
\( t=0 \) の時
\begin{eqnarray} h(t)= k_{1}(t+a) ・・・① k_{1}:比例定数 \end{eqnarray} 除雪車の時間あたりの作業は一定なので
\begin{eqnarray} v(t) × h(t) = k_{2} ・・・② k_{2}:比例定数 \end{eqnarray}
①を②に代入すると
\begin{eqnarray} v(t) × k_{1}(t+a) = k_{2} \end{eqnarray}
\begin{eqnarray}v(t) = \frac {k_{2}}{k_{1} (t+a)} = \frac {k_{3}}{ (t+a)} ・・・③ k_{3}= \frac {k_{2}}{k_{1} }:比例定数 \end{eqnarray}
ここで、速度を時間で積分すると、距離となることから、③を時間で積分すると
\begin{eqnarray}x(t) = \int v(t)dt= \int \frac {k_{3}}{ (t+a)}dt = k_{3} \int \frac {dt}{ (t+a)} \end{eqnarray}
\begin{eqnarray} = k_{3} \log { (t+a)+C} (C:積分定数)・・・④ \end{eqnarray}
ここで、正午⇒午前2時までに除雪したのは2(マイル)なので、
\begin{eqnarray}2 = x(1)-x(0) \end{eqnarray}
\begin{eqnarray} = k_{3} \log { (1+a)+C} – ( k_{3} \log a+C )\end{eqnarray}
\begin{eqnarray} = k_{3} ( \log (1+a) -\log a ) = k_{3} \log \frac {1+a}{a}・・・⑤ \end{eqnarray}
午後1時から2時までに除雪したのは1(マイル)なので、
\begin{eqnarray}1 = x(2)-x(1) \end{eqnarray}
\begin{eqnarray} = k_{3} \log { (2+a)+C} – ( k_{3} \log (1+ a)+C )\end{eqnarray}
\begin{eqnarray} = k_{3} \log \frac {2+a}{1+a} ・・・⑥ \end{eqnarray}
⑤、⑥式より、⑥式の両辺を2倍すると。
\begin{eqnarray} 2= 2 k_{3} \log \frac {2+a}{1+a} \end{eqnarray}
\begin{eqnarray} = k_{3} \log ( \frac {2+a}{1+a})^2 ・・・⑥’ \end{eqnarray}
⑤=⑥’より
\begin{eqnarray} k_{3} \log \frac {1+a}{a} = k_{3} \log ( \frac {2+a}{1+a})^2 \end{eqnarray}
log を取ると
\begin{eqnarray} \frac {1+a}{a} = ( \frac {2+a}{1+a})^2 \end{eqnarray}
\begin{eqnarray} (1+a)^3 = a(2+a)^2 \end{eqnarray}
\begin{eqnarray} a^3+3a^2+3a+1=a^3+4a^2+4a \end{eqnarray}
\begin{eqnarray} a^2+a-1=0 \end{eqnarray}
\begin{eqnarray} a= \frac {-1 \pm \sqrt{5}}{2} \end{eqnarray}
a>0より
\begin{eqnarray} a= \frac { \sqrt{5} -1 }{2} = \frac { 2.236 -1 }{2} =0.618 \end{eqnarray}
時間を分に直すと、 60(分)×0.618 = 37.08(分)
ですので、37分間に雪は降りはじめたので、求める答えは
午前11時23分
【解説】

【解説(手書き)】


【解説PDF(手書き)】



コメント