質量 \(M\) の人工衛星Pと質量 \(m\)(\(M\) >(1+\(\sqrt{2}\))\(m\))の物体 Q が、はじめ一体となって、地球の中心 \(O\) を中心とする半径\(r_{1}\)の等速円運動をしている。この円軌道上のある点で、人工衛星Pから物体Qを瞬間的に発射する。なお、発射の時の火薬の質量の減少は無視できるものとする。万有引力定数を \(G\) とし、地球の半径及び質量をそれぞれ \(R\) , \(M\) とする。人工衛星Pおよび物体Qの大きさ、P,Q間の相互作用,大気の影響および他の天体の影響などは全て無視しうるものとして、次の【A】および【B】それぞれの場合について設問に答えよ。なお、答えのみでなく、解法も簡潔に記載せよ。
【 A 】
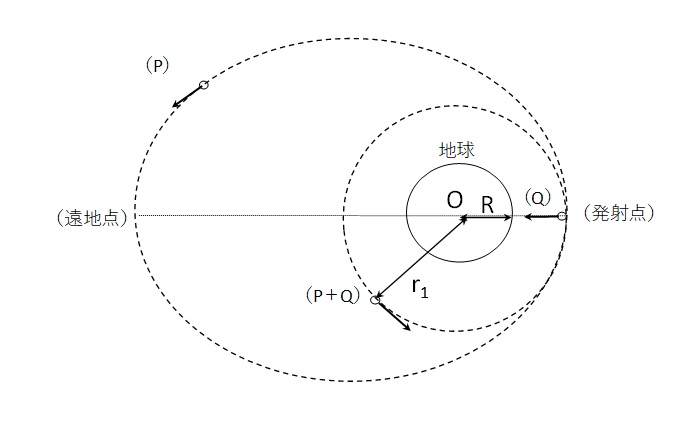
ある瞬間に、人工衛星Pの進行方向から見て後方に物体Qを発射すると、Qは地球(静止系)に対し、初速度0で地表に落下し始めた。また、人工衛星Pはその後、図のように発射点を近地点とする楕円軌道を描く。
(1)はじめの等速円運動の速さ\(v_{0}\)はいくらか
(2)発射の瞬間に火薬の爆発によって生じた力学的エネルギーはいくらか。\(v_{0}\)を用いて答えよ。
(3)物体Qが地表に達する直前のQの速さはいくらか
(4)人工衛星Pが楕円軌道上の遠地点(Oに関して発射点とちょうど反対側にある楕円軌道の点)に達した瞬間の速さはいくらか。\(v_{0}\)を用いて答えよ。
(5)(4)における遠地点距離を\(r_{2}\)とすると、この楕円運動の周期はいくらか。\(v_{0}\)を用いて答えよ。
【 B 】
ある瞬間に、人工衛星Pから見てその進行方向に物体Qを発射したとする。このとき、人工衛星Pは発射点を遠地点とする楕円軌道を描き始める。
(6)物体Qが無限遠方へ飛び去るための最小の発射直後のQの速さはいくらか。
(7)発射の瞬間に生じた力学的エネルギーが設問(2)の値で同じであるとき、物体Qは無限遠方へ飛び去ることが出来るかどうか。理由を記して答えよ。
【問題PDF】
【解説】



【解説PDF】




コメント