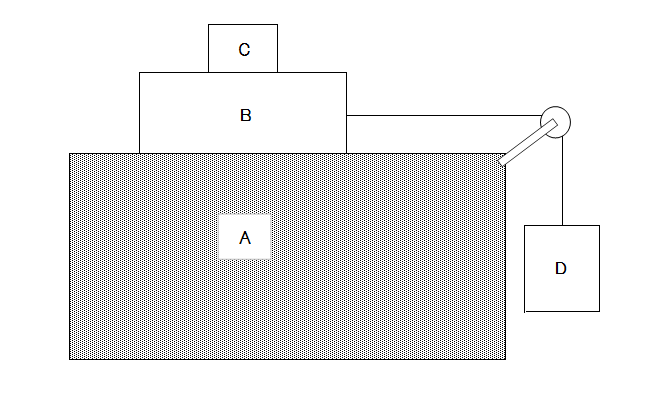
図1
図1のように、水平な台Aの上に、質量2\(m\)の直方体の物体Bを置き、その上に質量\(m\)の同じく直方体の物体Cを置く。 物体Bは、なめらかに回転する軽い滑車を通して水平にかけた軽い糸で質量\(x\)の物体Dと繋がっている。この糸は伸び縮みしない。また、質量\(x\)は0から増やせるようになっている。
\(x\)が質量\(m_{1}\)以下のときは、物体B,C,Dは動かないが、\(x\)が質量\(m\)(\(m_{1}\)<\(m_{2}\))より大きくなると、物体B,Cは別々に動き始める。 物体B,Cが一体となり物体Dと同じ加速度 \(α\)で運動するとき、つまり\(m_{1}\)<\(x\)≦\(m_{2}\)のときの、物体間の摩擦力や糸の張力、加速度\(α\)や質量\(m_{2}\)の値を求めたい。
重力加速度の大きさを\(g\)とし、台Aと物体Bの間には静止摩擦係数\(μ\)と運動摩擦係数\(μ\)’(\(μ\)\(μ\)’)で特徴づけられる摩擦力\(F\)が、物体Bと物体Cの間にも同じ摩擦力\(f\)が働いているものとする。また、糸の張力を\(T\)とする。
問題において、それぞれ文章中の\(m\),\(x\),\(g\),\(μ\),\(μ\)’の中から必要な記号を用いて解答しなさい。問2は、文章中の\(T\),\(f\)を加えた記号の中から必要な記号を用いて解答しなさい。
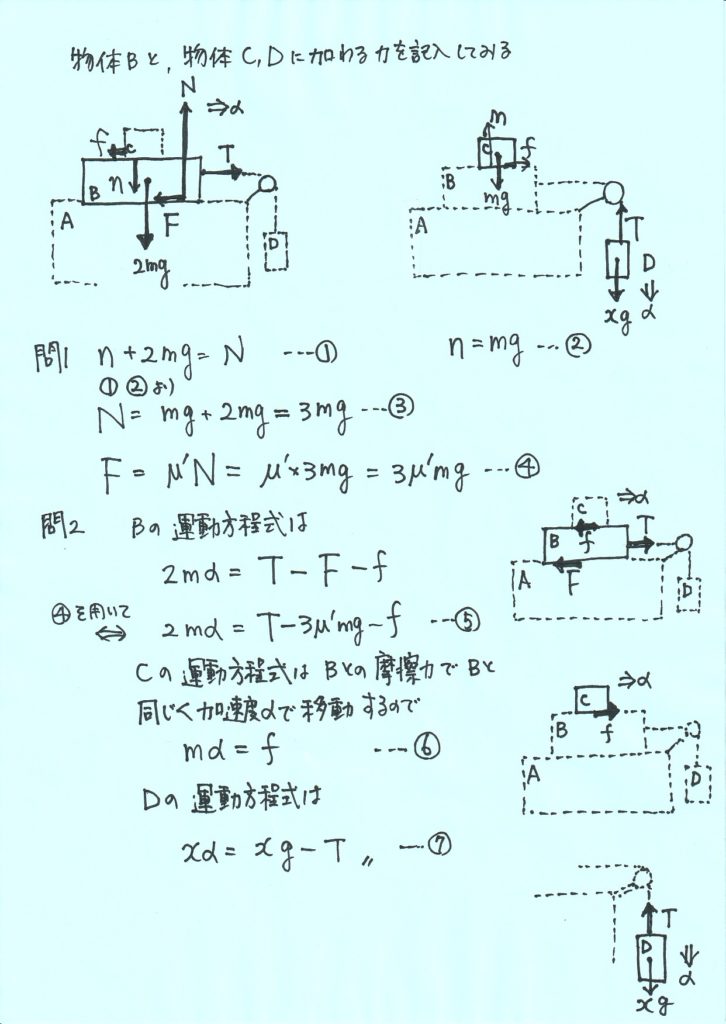
問1 \(F\)を示せ。
問2 物体B,C,Dの運動方程式を示せ。
問3 運動方程式より、 加速度\(α\),張力\(T\),摩擦力\(f\)を求めよ。
問4 \(x\)=\(m_{2}\)のとき、\(f\)は最大静止摩擦力に達する。その時のfを求めよ。
その時の加速度\(α\)とDの質量\(m_{2}\)を求めよ。
(旭川医科大学)
【問題PDF】
【解説】

【解説PDF】



コメント